Pentagonal-grand hendecagrammic duoprism

Pentagonal-grand hendecagrammic duoprism
	(OFF file)
Rank	4
Type	Uniform
Notation
Coxeter diagram	x5o x11/5o ()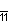
Elements
Cells	11 pentagonal prisms, 5 grand hendecagrammic prisms
Faces	55 squares, 11 pentagons, 5 grand hendecagrams
Edges	55+55
Vertices	55
Vertex figure	Digonal disphenoid, edge lengths (1+√5)/2 (base 1), 2cos(5π/11) (base 2), √2 (sides)
Measures (edge length 1)
Circumradius
Hypervolume
Dichoral angles	Gashenp–11/5–gashenp: 108°
	Pip–4–gashenp: 90°
	Pip–5–pip:
Central density	5
Number of external pieces	27
Level of complexity	12
Related polytopes
Army	Semi-uniform pahendip
Dual	Pentagonal-grand hendecagrammic duotegum
Conjugates	Pentagonal-hendecagonal duoprism, Pentagonal-small hendecagrammic duoprism, Pentagonal-hendecagrammic duoprism, Pentagonal-great hendecagrammic duoprism, Pentagrammic-hendecagonal duoprism, Pentagrammic-small hendecagrammic duoprism, Pentagrammic-hendecagrammic duoprism, Pentagrammic-great hendecagrammic duoprism, Pentagrammic-grand hendecagrammic duoprism
Abstract & topological properties
Euler characteristic	0
Orientable	Yes
Properties
Symmetry	H2×I2(11), order 220
Convex	No
Nature	Tame

The pentagonal-grand hendecagrammic duoprism, also known as the 5-11/5 duoprism, is a uniform duoprism that consists of 11 pentagonal prisms and 5 grand hendecagrammic prisms, with two of each at each vertex.

Vertex coordinates[edit | edit source]

The coordinates of a pentagonal-grand hendecagrammic duoprism, centered at the origin and with edge length 2sin(5π/11), are given by:

$\left(\pm \sin {\frac {5\pi }{11}},\,-{\sqrt {\frac {5+2{\sqrt {5}}}{5}}}\sin {\frac {5\pi }{11}},\,1,\,0\right),$
$\left(\pm \sin {\frac {5\pi }{11}},\,-{\sqrt {\frac {5+2{\sqrt {5}}}{5}}}\sin {\frac {5\pi }{11}},\,\cos \left({\frac {j\pi }{11}}\right),\,\pm \sin \left({\frac {j\pi }{11}}\right)\right),$
$\left(\pm {\frac {1+{\sqrt {5}}}{2}}\sin {\frac {5\pi }{11}},\,{\sqrt {\frac {5-{\sqrt {5}}}{10}}}\sin {\frac {5\pi }{11}},\,1,\,0\right),$
$\left(\pm {\frac {1+{\sqrt {5}}}{2}}\sin {\frac {5\pi }{11}},\,{\sqrt {\frac {5-{\sqrt {5}}}{10}}}\sin {\frac {5\pi }{11}},\,\cos \left({\frac {j\pi }{11}}\right),\,\pm \sin \left({\frac {j\pi }{11}}\right)\right),$
$\left(0,\,2{\sqrt {\frac {5+{\sqrt {5}}}{10}}}\sin {\frac {5\pi }{11}},\,1,\,0\right),$
$\left(0,\,2{\sqrt {\frac {5+{\sqrt {5}}}{10}}}\sin {\frac {5\pi }{11}},\,\cos \left({\frac {j\pi }{11}}\right),\,\pm \sin \left({\frac {j\pi }{11}}\right)\right),$