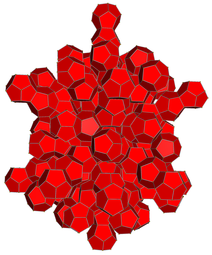
Hecatonicosachoron
| Hecatonicosachoron | |
|---|---|
 | |
| Rank | 4 |
| Type | Regular |
| Notation | |
| Bowers style acronym | Hi |
| Coxeter diagram | x5o3o3o ( |
| Schläfli symbol | {5,3,3} |
| Elements | |
| Cells | 120 dodecahedra |
| Faces | 720 pentagons |
| Edges | 1200 |
| Vertices | 600 |
| Vertex figure | Tetrahedron, edge length (1+√5)/2  |
| Edge figure | doe 5 doe 5 doe 5 |
| Measures (edge length 1) | |
| Circumradius | |
| Edge radius | |
| Face radius | |
| Inradius | |
| Hypervolume | |
| Dichoral angle | 144° |
| Central density | 1 |
| Number of external pieces | 120 |
| Level of complexity | 1 |
| Related polytopes | |
| Army | Hi |
| Regiment | Hi |
| Dual | Hexacosichoron |
| κ ? | Kappa 120-cell |
| Conjugate | Great grand stellated hecatonicosachoron |
| Abstract & topological properties | |
| Flag count | 14400 |
| Euler characteristic | 0 |
| Orientable | Yes |
| Properties | |
| Symmetry | H4, order 14400 |
| Convex | Yes |
| Nature | Tame |
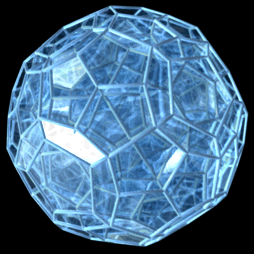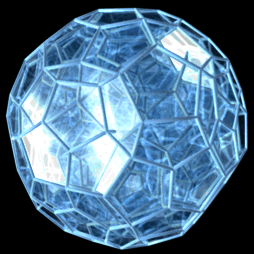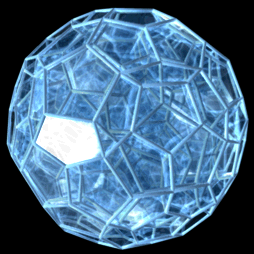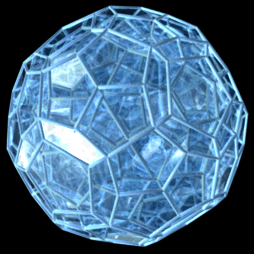
The hecatonicosachoron, or hi, also commonly called the 120-cell, is one of the 6 convex regular polychora. It has 120 dodecahedra as cells, joining 3 to an edge and 4 to a vertex.
It is the first in an infinite family of isochoric dodecahedral swirlchora (the dodecaswirlic hecatonicosachoron), as its cells form 12 rings of 10 cells. It is also the first in a series of isochoric rhombic triacontahedral swirlchora (the rhombitriacontaswirlic hecatonicosachoron).
Gallery[edit | edit source]
-
Rotating hecatonicosachoron
-
Net
-
Cross-section animation
Vertex coordinates[edit | edit source]
The vertices of a hecatonicosachoron of edge length 1, centered at the origin, are given by all permutations of:
- ,
- ,
- ,
- ,
together with all the even permutations of:
- ,
- ,
- .
Surtope angles[edit | edit source]
This section may require cleanup to meet Polytope Wiki's quality standards. The specific problem is: This is Wendy nonsense. (Learn how and when to remove this template message) |
The surtope angle represents the fraction of solid space occupied by the angle.
- A2: 0:48.00.00 = 144° =2/5 Dichoral or Margin angle. There is a decagon of dodecahedra girthing the figure.
- A3: 0:42.00.00 = 252° E =7/20
- A4: 0:38.24.00 = 191/600
The higher order angles might be derived from the tiling x5o3o3o5/2o (![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ), which is piecewise-finite (i.e. any surtope can be 'completed').
), which is piecewise-finite (i.e. any surtope can be 'completed').
Representations[edit | edit source]
A hecatonicosachoron has the following Coxeter diagrams:
- x5o3o3o (






 ) (full symmetry)
) (full symmetry) - xofoFofFxFfBo5oxofoFfxFfFoB BoFfFxfoFofox5oBfFxFfFofoxo&#zx (H2×H2 symmetry)
- ooCfoBxoFf3oooooofffx3CooBfoFxof *b3oCooBfoFxf&#zx (D4 symmetry, C=2F)
- xfooofFxFfooofx5oofxfooooofxfoo3ooofxfoFofxfooo&#xt (H3 axial, cell-first)
Related polychora[edit | edit source]
Uniform polychoron compounds composed of hecatonicosachora include:
Isogonal derivatives[edit | edit source]
Substitution by vertices of these following elements will produce these convex isogonal polychora:
- Dodecahedron (120): Hexacosichoron
- Pentagon (720): Rectified hexacosichoron
- Edge (1200): Rectified hecatonicosachoron
External links[edit | edit source]
- Bowers, Jonathan. "Category 1: Regular Polychora" (#5).
- Klitzing, Richard. "hi".
- Quickfur. "The 120-Cell".
- Nan Ma. "120-cell {5, 3, 3}".
- Wikipedia contributors. "120-cell".
- Hi.gher.Space Wiki Contributors. "Cosmochoron".
- Schläfli type 5,3,3
- Articles needing cleanup
- All pages needing cleanup
- Cleanup tagged articles with a reason field
- Polytope Wiki pages needing cleanup
- H4 symmetry
- Hi army
- Rhombic triacontahedral swirlchora
- Dodecahedral swirlchora
- Isogonal swirlchora
- Isochoric swirlchora
- Noble swirlchora
- Convex regular polychora
- Polychora with 120 cells