Pentachoron
| Pentachoron | |
|---|---|
 | |
| Rank | 4 |
| Type | Regular |
| Notation | |
| Bowers style acronym | Pen |
| Coxeter diagram | x3o3o3o ( |
| Schläfli symbol | {3,3,3} |
| Tapertopic notation | 13 |
| Elements | |
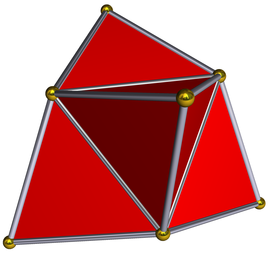
| Cells | 5 tetrahedra |
| Faces | 10 triangles |
| Edges | 10 |
| Vertices | 5 |
| Vertex figure | Tetrahedron, edge length 1  |
| Edge figure | tet 3 tet 3 tet 3 |
| Petrie polygons | 12 pentagonal-pentagrammic coils |
| Measures (edge length 1) | |
| Circumradius | |
| Edge radius | |
| Face radius | |
| Inradius | |
| Hypervolume | |
| Dichoral angle | |
| Heights | Point atop tet: |
| Dyad atop perp trig: | |
| Central density | 1 |
| Number of external pieces | 5 |
| Level of complexity | 1 |
| Related polytopes | |
| Army | Pen |
| Regiment | Pen |
| Dual | Pentachoron |
| Conjugate | None |
| Abstract & topological properties | |
| Flag count | 120 |
| Euler characteristic | 0 |
| Orientable | Yes |
| Properties | |
| Symmetry | A4, order 120 |
| Convex | Yes |
| Nature | Tame |
The pentachoron, or pen, also commonly called the 5-cell or the 4-simplex, is the simplest possible non-degenerate polychoron. The full symmetry version has 5 regular tetrahedra as cells, joining 3 to an edge and 4 to a vertex, and is one of the 6 convex regular polychora. It is the 4-dimensional simplex.
In addition, it can also be considered to be the regular-faced pyramid of the tetrahedron, or the pyramid product of a triangle and a dyad. This makes it the simplest segmentochoron as well, and it is designated K-4.1 in Richard Klitzing's list of convex segmentochora. It is also the 5-2 step prism and gyrochoron.
Gallery[edit | edit source]
-
Rotating pentachoron
-
Cross-section animation
-
Wireframe, cell, net
Vertex coordinates[edit | edit source]
The vertices of a regular pentachoron of edge length 1, centered at the origin, are given by:
- ,
- ,
- ,
- .
Much simpler coordinates can be given in five dimensions, as all permutations of:
- .
A further set of coordinates, derived from the 5-2 step prism construction, is given by:
- ,
- ,
together with reflections through the and the hyperplanes.
Representations[edit | edit source]
A pentachoron has the following Coxeter diagrams:
- x3o3o3o (






 ) (full symmetry)
) (full symmetry) - ox3oo3oo&#x (A3 axial, as tetrahedral pyramid)
- xo ox3oo&#x (A2×A1 axial, as triangle-dyad disphenoid)
- oox3ooo&#x (A2 axial, as triangular scalene)
- oxo oox&#x (A1×A1 axial, as disphenoidal pyramid)
- ooox&#x (bilateral symmetry only)
- ooooo&#x (no symmetry)
Variations[edit | edit source]
Besides the regular pentachoron, various other types of pentachora exist, some of which occur in vertex figures. These include:
- Tetrahedral pyramid - 1 regular tetrahedron, 4 triangular pyramids, tetrahedral symmetry
- Triangular scalene - 2 triangular pyramids, 3 digonal disphenoids, triangular prismatic axial symmetry
- Triangular pyramidal pyramid - 2 different triangular pyramids, 3 sphenoids, triangular symmetry
- Tetragonal disphenoidal pyramid - 1 tetragonal disphenoid, 4 sphenoids, digonal antiprismatic axial symmetry
- Rhombic disphenoidal pyramid - 1 rhombic disphenoid, 4 irregular tetrahedra, chiral digonal prismatic axial symmetry
- Digonal disphenoidal pyramid - 1 digonal disphenoid, 2 pairs of sphenoids, digonal axial symmetry
- Sphenoidal pyramid - 2 identical irregular tetrahedra, 3 different sphenoids
- Phyllic disphenoidal pyramid - 1 phyllic dissphenoid, 2 pairs of identical irregular tetrahedra, bilateral symmetry
- Irregular pentachoron - no symmetry, 5 different irregular tetrahedra
- 5-2 step prism (or gyrochoron) noble, 5 phyllic disphenoids
Related polychora[edit | edit source]
Two pentachora can be attached at a common cell to form the tetrahedral tegum.
Uniform polychoron compounds composed of pentachora include:
- Stellated decachoron (2)
- Gyrosimplexifissal icosachoron (4)
- Chirosimplexifissal icosipentachoron (5)
- Simplexifissial disicosipentachoron (10)
- Compound of 12 pentachora (12)
- Medial hexacosichoron (120)
- Compound of 720 pentachora (720)
- An infinite family of gyrochoron-symmetric compounds
Isogonal derivatives[edit | edit source]
Substitution by vertices of these following elements will produce these convex isogonal polychora:
- Tetrahedron (5): Pentachoron
- Triangle (10): Rectified pentachoron
- Edge (10): Rectified pentachoron
External links[edit | edit source]
- Bowers, Jonathan. "Category 1: Regular Polychora" (#1).
- Bowers, Jonathan. "Four Dimensional Dice Up To Twenty Sides".
- Bowers, Jonathan. "Pennic and Decaic Isogonals".
- Klitzing, Richard. "Pen".
- Quickfur. "The Pentachoron".
- Wikipedia contributors. "5-cell".
- Hartley, Michael. "{3,3,3}*120".