Pentagram
| Pentagram | |
|---|---|
| Rank | 2 |
| Type | Regular |
| Notation | |
| Bowers style acronym | Star |
| Coxeter diagram | x5/2o ( |
| Schläfli symbol | {5/2} |
| Elements | |
| Edges | 5 |
| Vertices | 5 |
| Vertex figure | Dyad, length (√5–1)/2 |
| Measures (edge length 1) | |
| Circumradius | |
| Inradius | |
| Area | |
| Angle | 36° |
| Central density | 2 |
| Number of external pieces | 10 |
| Level of complexity | 2 |
| Related polytopes | |
| Army | Peg, edge length |
| Dual | Pentagram |
| Conjugate | Pentagon |
| Convex core | Pentagon |
| Abstract & topological properties | |
| Flag count | 10 |
| Euler characteristic | 0 |
| Orientable | Yes |
| Properties | |
| Symmetry | H2, order 10 |
| Flag orbits | 1 |
| Convex | No |
| Nature | Tame |
The pentagram is a non-convex polygon with 5 sides and the simplest star regular polygon. A regular pentagram has equal sides and equal angles.
This is the only stellation of the pentagon. The only other polygons with a single non-compound stellation are the octagon, the decagon, and the dodecagon.
Pentagrams occur as faces in two of the four Kepler-Poinsot solids, namely the small stellated dodecahedron and great stellated dodecahedron.
Vertex coordinates[edit | edit source]
Coordinates for the vertices of a regular pentagram of unit edge length, centered at the origin, are:
- ,
- ,
- .
Representations[edit | edit source]
A regular pentagram has the following Coxeter diagrams:
- x5/2o (

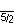
 )
) - ß5o (
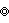

 ) (as holosnub pentagon)
) (as holosnub pentagon)
In vertex figures[edit | edit source]
The regular pentagram appears as a vertex figure in two uniform polyhedra, namely the great icosahedron (with an edge length of 1) and the great dodecahedron (with an edge length of (1+√5)/2). Irregular pentagrams further appear as the vertex figures of some snub polyhedra.
External links[edit | edit source]
- Bowers, Jonathan. "Regular Polygons and Other Two Dimensional Shapes".
- Klitzing, Richard. "Polygons"
- Nan Ma. "Pentagram {5/2}".
- Wikipedia contributors. "Pentagram".
- Hartley, Michael. "{5}*10".






