Bilunabirotunda
| Bilunabirotunda | |
|---|---|
 | |
| Rank | 3 |
| Type | CRF |
| Notation | |
| Bowers style acronym | Bilbiro |
| Coxeter diagram | xfofx oxfxo&#xt |
| Stewart notation | J91 |
| Elements | |
| Faces | 4+4 triangles, 2 squares, 4 pentagons |
| Edges | 2+4+4+8+8 |
| Vertices | 2+4+8 |
| Vertex figures | 4 scalene triangles, edge lengths 1, (1+√5}/2, (1+√5)/2 |
| 2 rectangles, edge lengths 1 and (1+√5)/2 | |
| 8 irregular tetragons, edge lengths 1, √2, 1, (1+√5)/2 | |
| Measures (edge length 1) | |
| Volume | |
| Dihedral angles | 3–4 lunaic: |
| 3–5 rotundaic: | |
| 3–4 medial: | |
| 3–5 join: | |
| 5–5: | |
| Central density | 1 |
| Number of external pieces | 14 |
| Level of complexity | 26 |
| Related polytopes | |
| Army | Bilbiro |
| Regiment | Bilbiro |
| Dual | Parabisected rhombic dodecahedron |
| Conjugate | Great bilunabirotunda |
| Abstract & topological properties | |
| Flag count | 104 |
| Euler characteristic | 2 |
| Surface | Sphere |
| Orientable | Yes |
| Genus | 0 |
| Properties | |
| Symmetry | K3, order 8 |
| Convex | Yes |
| Nature | Tame |
The bilunabirotunda is one of the 92 Johnson solids (J91). It consists of 4+4 triangles, 2 squares, and 4 pentagons.
It is one of several polyhedra near the end of the list of Johnson solids with no obvious relation to the uniform polyhedra. However, there are various connections to other polyhedra. Most notably, both 3.5.3.5 vertices have the exact same configuration as the icosidodecahedron, joining two triangles and two pentagons at the same angles. The "birotunda" in the name refers to these two areas, while the "biluna" refers to the two lunes (sections with a square connecting to two triangles). The lunes are identical to those of the small rhombicosidodecahedron, thus making the 3.4.3.5 vertices identical to those of the pentagonal orthocupolarotunda. The 3.5.5 vertices are identical to those of the metabidiminished and tridiminished icosahedra.
If the "rotunda" parts of two bilunabirotundae are aligned with opposite corresponding parts of an icosidodecahedron, they touch at the center of the icosidodecahedron because each bilunabirotunda's altitude in this direction is exactly half that of the icosidodecahedron. If the "lune" parts of two bilunabirotundae are aligned with opposite parts of a small rhombicosidodecahedron, a cube can be placed in between the bilunabirotundae because the small rhombicosidodecahedron's square-to-square altitude is , exactly the same as the combined square-to-square height of a cube and two bilunabirotundae.
The bilunabirotunda also has a connection with the regular icosahedron, being a partial Stott expansion of a digonal-symmetric faceting of the icosahedron. Similarly, the bilunabirotunda can be formed by removing the pentagonal pyramids from a Minkowski sum of an icosahedron and a dyad parallel and equal in length to one of the icosahedron's edges.
If the two pentagon-pentagon edges are contracted to points, turning the pentagons to squares, the result is a cuboctahedron.
Vertex coordinates[edit | edit source]
A bilunabirotunda of edge length 1 has vertices given by the following coordinates:
Related polyhedra[edit | edit source]
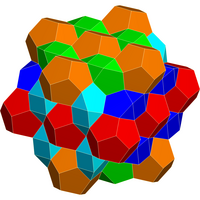
The bilunabirotunda can tile Euclidean 3-space alongside cubes and regular dodecahedra.
External links[edit | edit source]
- Klitzing, Richard. "bilbiro".
- Quickfur. "The Bilunabirotunda".
- Wikipedia contributors. "Bilunabirotunda".
- Hi.gher.Space Wiki Contributors. "Bilunabirotunda".
- McCooey, David. "Bilunabirotunda"