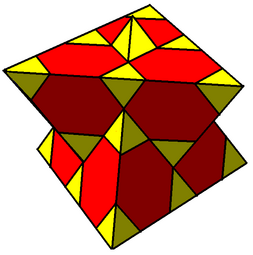
Cyclotruncated tetrahedral-octahedral honeycomb

Cyclotruncated tetrahedral-octahedral honeycomb
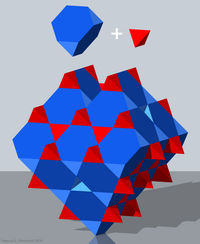Rank	4
Type	Uniform
Space	Euclidean
Notation
Bowers style acronym	Cytatoh (old: Batatoh)
Coxeter diagram	x3x3o3o3*a ()
Elements
Cells	N tetrahedra, N truncated tetrahedra
Faces	4N triangles, 2N hexagons
Edges	6N
Vertices	2N
Vertex figure	Triangular antiprism, edge lengths 1 (base) and √3 (sides)
Measures (edge length 1)
Vertex density	${\frac {\sqrt {2}}{2}}\approx 0.70710678119$
Related polytopes
Army	Cytatoh
Regiment	Cytatoh
Dual	Triangular antitegmatic honeycomb
Conjugate	None
Abstract & topological properties
Orientable	Yes
Properties
Symmetry	P4×2
Convex	Yes
Nature	Tame

The cyclotruncated tetrahedral-octahedral honeycomb, also known as the quarter cubic honeycomb, is a convex uniform honeycomb. 2 tetrahedra and 6 truncated tetrahedra join at each vertex of this honeycomb. It can be formed by applying two successive alternated faceting to the cubic honeycomb. It is related to the mutetrahedron, whose faces are exactly its hexagonal faces.

Representations

A cyclotruncated tetrahedral-octahedral honeycomb has the following Coxeter diagrams:

• x3x3o3o3*a () (full symmetry)
• s4o3x o3*b () (as single alternated faceting)
• β4o3o4s () (as double alternated faceting)

Gallery

• 

  Wireframe

• 

  Slab

• 

External links

• Klitzing, Richard. "cytatoh".
• Wikipedia contributors. "Quarter cubic honeycomb".
• Binnendyk, Eric. "Category 7: Triangular Podiumverts" (#140).