Ditrigonary dodecadodecahedron
| Ditrigonary dodecadodecahedron | |
|---|---|
 | |
| Rank | 3 |
| Type | Uniform |
| Notation | |
| Bowers style acronym | Ditdid |
| Coxeter diagram | x5/3o3o5*a ( |
| Schläfli symbol | |
| Elements | |
| Faces | 12 pentagons, 12 pentagrams |
| Edges | 60 |
| Vertices | 20 |
| Vertex figure | Tripod, edge lengths (√5–1)/2 and (1+√5)/2  |
| Petrie polygons | 30 skew rhombi |
| Measures (edge length 1) | |
| Circumradius | |
| Volume | 0 |
| Dihedral angle | |
| Central density | 4 |
| Number of external pieces | 192 |
| Level of complexity | 11 |
| Related polytopes | |
| Army | Doe, edge length |
| Regiment | Sidtid |
| Dual | Medial triambic icosahedron |
| Conjugate | Ditrigonary dodecadodecahedron |
| Convex core | Dodecahedron |
| Abstract & topological properties | |
| Flag count | 240 |
| Euler characteristic | –16 |
| Schläfli type | {5,6} |
| Orientable | Yes |
| Genus | 9 |
| Properties | |
| Symmetry | H3, order 120 |
| Flag orbits | 2 |
| Convex | No |
| Nature | Tame |
The ditrigonary dodecadodecahedron, or ditdid, is a quasiregular uniform polyhedron. It consists of 12 pentagons and 12 pentagrams, with three of each joining at a vertex.
It is a faceting of the small ditrigonary icosidodecahedron, using its 12 pentagrams along with 12 additional pentagons.
This polyhedron is abstractly regular, being a quotient of the order-6 pentagonal tiling. Among the non-regular uniform polytopes, it shares this property with the dodecadodecahedron. Its realization may also be considered regular if one also counts conjugacies as symmetries.
This polyhedron is the vertex figure of the ditrigonary dishecatonicosachoron.
Vertex coordinates[edit | edit source]
Its vertices are the same as those of its regiment colonel, the small ditrigonary icosidodecahedron.
Related polyhedra[edit | edit source]
| Name | OBSA | CD diagram | Picture |
|---|---|---|---|
| Ditrigonary dodecadodecahedron | ditdid |  | |
| Small complex icosidodecahedron (degenerate, ike+gad) | cid | ||
| Great complex icosidodecahedron (degenerate, sissid+gike) | gacid |  | |
| Icosidodecadodecahedron | ided |  | |
| Small ditrigonal dodecicosidodecahedron | sidditdid | 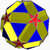 | |
| Great ditrigonal dodecicosidodecahedron | gidditdid |  | |
| Icosidodecatruncated icosidodecahedron | idtid |  | |
| Snub icosidodecadodecahedron | sided |  |
External links[edit | edit source]
- Bowers, Jonathan. "Polyhedron Category 3: Quasiregulars" (#34).
- Klitzing, Richard. "ditdid".
- Wikipedia contributors. "Ditrigonal dodecadodecahedron".
- McCooey, David. "Ditrigonal Dodecadodecahedron"
- Hartley, Michael. "{5,6}*240a".




