Blending

This article is about an operation which generalizes the symmetric difference of sets. For other uses, see Blending (disambiguation).

An inner blend of two triangular prisms at a square face. An outer blend of the same would produce the gyrobifastigium.

Blending is a polytope operation in which two or more polytopes of the same rank are "glued together" at pairs of facets or other elements, which are removed from the resulting polytope.

Definition

Given a set of polytopes (again with the same rank and positioned in the same ambient space), their blend is defined as the result of the following operations:

1. Combine the polytopes together to form a compound.
2. Find all pairs of coplanar facets.
3. For each pair, if they coincide completely, remove them, otherwise blend them.
4. Remove any lower-rank elements that are not adjacent to any facets. (This can happen if any two removed facets were adjacent in the original polytopes.)

In the simplest case, no facets are coincident and a compound is formed (but this is usually not called a "blend"). At the other extreme, blending a polytope with a copy of itself in the same position and orientation results in an empty polytope. A blend is not guaranteed to be dyadic, this can happen for example by blending two polyhedra that share an edge.

Note that the definition does not actually require two or more polytopes. It is possible to blend a single polytope which has coincident facets. Such polytopes often appear from a non-convex Wythoffian construction or lace simplex, and in some frameworks the blend can be identified with the original polytope.

Inner and outer blends

The term "internal blend" or "inner blend" may be used when the centers of the blended-together polytopes are on the same side of the hyperplane that contained the removed facet. When the polytopes' centers are on opposite sides, it may be called an "external blend" or "outer blend."

An inner blend

Polytopes	Resultant blend
3 octagonal prisms oriented differently	Small rhombihexahedron
Six pairs of coincident square faces are removed. Coincident edges and vertices (belonging to those squares) are merged. (The octagonal faces intersect one another, but do not coincide.)

Augmentation

In the context of the Johnson solids, several specific varieties of blending are given names. Key among them is augmentation. For two polytopes, this involves a coincident pair of congruent facets being removed, as they end up inside the resultant polytope. Coincident edges, vertices, and other subdimensional elements are merged since they lie on the polytope's surface.

Diminishing can also be considered a type of blend, in which all but one facet of one polytope is removed. Consider the diminished icosahedron as a blend of an icosahedron and pentagonal pyramid. All of the pyramid's triangular faces become coincident with the icosahedron's faces and are thus removed (note that some sub-dimensional elements must be removed in addition to the coincident facets, unlike in augmentation), leaving only one of the pyramid's facets behind: its pentagon base. Diminishing can be thought of as the "subtraction" to augmenting's "addition".

An augmentation performed in the opposite direction is sometimes referred to as an "excavation", as seen in the excavated dodecahedron. In layman's terms, the difference is that an augmentation "adds material" while an excavation "subtracts" it. A diminishment that adds material is called a replenishment, as seen in the trireplenished great icosahedron. Excavations and diminishings would technically be classified as inner blends, because both of the used polytopes' centers lie on the same side of the coincident facet's hyperplane.

An augmentation or outer blend

Polytope 1	Polytope 2	Resultant blend
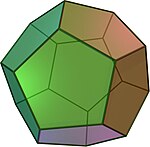
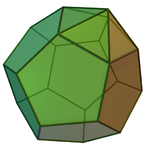
Dodecahedron	Pentagonal pyramid	Augmented dodecahedron
The coincident pentagonal faces end up on the inside and are removed. Ten pairs of coincident edges and vertices end up on the outside and are merged.

External links

• Klitzing, Richard. Compound.