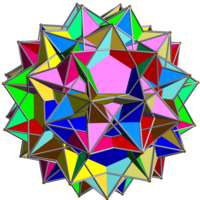
Compound of twelve pentagrammic prisms

Compound of twelve pentagrammic prisms
	(OFF file)
Rank	3
Type	Uniform
Notation
Bowers style acronym	Giddird
Elements
Components	12 pentagrammic prisms
Faces	60 squares, 24 pentagrams
Edges	60+120
Vertices	60
Vertex figure	Compound of two isosceles triangles, edge lengths (√5–1)/2, √2, √2
Measures (edge length 1)
Circumradius
Volume
Dihedral angles	4–5/2: 90°
	4–4: 36°
Central density	24
Number of external pieces	672
Level of complexity	42
Related polytopes
Army	Srid, edge length
Regiment	Giddird
Dual	Compound of twelve pentagrammic tegums
Conjugate	Compound of twelve pentagonal prisms
Convex core	Rhombic triacontahedron
Abstract & topological properties
Flag count	720
Orientable	Yes
Properties
Symmetry	H3, order 120
Convex	No
Nature	Tame

The great disrhombidodecahedron, giddird, or compound of twelve pentagrammic prisms is a uniform polyhedron compound. It consists of 60 squares and 24 pentagrams, with two pentagrams and four squares joining at a vertex.

It can be formed by combining the two chiral forms of the great chirorhombidodecahedron, which results in vertices pairing up and two components joining per vertex.

Its quotient prismatic equivalent is the pentagrammic prismatic dodecadakoorthowedge, which is fourteen-dimensional.

Vertex coordinates[edit | edit source]

The vertices of a great disrhombidodecahedron of edge length 1 are given by all permutations of:

$\left(\pm {\sqrt {\frac {5+2{\sqrt {5}}}{20}}},\,\pm {\sqrt {\frac {5-2{\sqrt {5}}}{20}}},\,\pm {\sqrt {\frac {5-2{\sqrt {5}}}{20}}}\right)$ ,

plus all even permutations of:

$\left(0,\,\pm {\sqrt {\frac {5+{\sqrt {5}}}{40}}},\,\pm {\sqrt {\frac {5-{\sqrt {5}}}{8}}}\right)$ ,
$\left(\pm {\sqrt {\frac {5+{\sqrt {5}}}{40}}},\,\pm {\sqrt {\frac {5-{\sqrt {5}}}{40}}},\,\pm {\sqrt {\frac {5-{\sqrt {5}}}{10}}}\right)$ .