Great ditrigonary icosidodecahedron
(Redirected from Great ditrigonal icosidodecahedron)
| Great ditrigonary icosidodecahedron | |
|---|---|
 | |
| Rank | 3 |
| Type | Uniform |
| Notation | |
| Bowers style acronym | Gidtid |
| Coxeter diagram | o5x3/2o3*a ( |
| Elements | |
| Faces | 20 triangles, 12 pentagons |
| Edges | 60 |
| Vertices | 20 |
| Vertex figure | Tripod, edge lengths 1 and (1+√5)/2  |
| Measures (edge length 1) | |
| Circumradius | |
| Volume | |
| Dihedral angle | |
| Central density | 6 |
| Number of external pieces | 300 |
| Level of complexity | 15 |
| Related polytopes | |
| Army | Doe, edge length |
| Regiment | Sidtid |
| Dual | Great triambic icosahedron |
| Conjugate | Small ditrigonary icosidodecahedron |
| Convex core | Dodecahedron |
| Abstract & topological properties | |
| Flag count | 240 |
| Euler characteristic | –8 |
| Orientable | Yes |
| Genus | 5 |
| Properties | |
| Symmetry | H3, order 120 |
| Flag orbits | 2 |
| Convex | No |
| Nature | Tame |
The great ditrigonary icosidodecahedron or gidtid is a quasiregular uniform polyhedron. It consists of 20 equilateral triangles and 12 pentagons, with three of each joining at a vertex.
It is a faceting of the small ditrigonary icosidodecahedron, using its 20 triangles along with 12 additional pentagons.
It can be constructed as a holosnub great stellated dodecahedron.
This polyhedron is the vertex figure of the great ditrigonary hexacosihecatonicosachoron.
Vertex coordinates[edit | edit source]
Its vertices are the same as those of its regiment colonel, the small ditrigonary icosidodecahedron.
Representations[edit | edit source]
A great ditrigonary icosidodecahedron has the following Coxeter diagrams:
- o5x3/2o3*a (


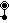
 )
) - ß5/2o3o (
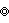
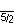


 ) (as holosnub)
) (as holosnub)
External links[edit | edit source]
- Bowers, Jonathan. "Polyhedron Category 3: Quasiregulars" (#35).
- Klitzing, Richard. "gidtid".
- Wikipedia contributors. "Great ditrigonal icosidodecahedron".
- McCooey, David. "Great Ditrigonal Icosidodecahedron"








