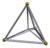
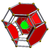
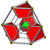
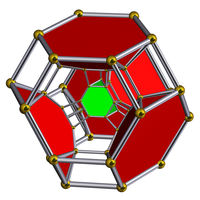
The great rhombated pentachoron , or grip , also commonly called the cantitruncated 5-cell or cantitruncated pentachoron , is a convex uniform polychoron that consists of 10 triangular prisms , 5 truncated tetrahedra , and 5 truncated octahedra . 1 triangular prism, 1 truncated tetrahedron, and 2 truncated octahedra join at each vertex. As one of its names suggests, it can be obtained by cantitruncating the pentachoron .
The vertices of a great rhombated pentachoron of edge length 1 are given by:
(
10
20
,
−
6
4
,
3
2
,
±
3
2
)
{\displaystyle \left({\frac {\sqrt {10}}{20}},\,-{\frac {\sqrt {6}}{4}},\,{\frac {\sqrt {3}}{2}},\,\pm {\frac {3}{2}}\right)}
(
10
20
,
−
6
4
,
−
3
,
0
)
{\displaystyle \left({\frac {\sqrt {10}}{20}},\,-{\frac {\sqrt {6}}{4}},\,-{\sqrt {3}},\,0\right)}
(
10
20
,
5
6
12
,
−
3
6
,
±
3
2
)
{\displaystyle \left({\frac {\sqrt {10}}{20}},\,{\frac {5{\sqrt {6}}}{12}},\,-{\frac {\sqrt {3}}{6}},\,\pm {\frac {3}{2}}\right)}
(
10
20
,
5
6
12
,
−
2
3
3
,
±
1
)
{\displaystyle \left({\frac {\sqrt {10}}{20}},\,{\frac {5{\sqrt {6}}}{12}},\,-{\frac {2{\sqrt {3}}}{3}},\,\pm 1\right)}
(
10
20
,
5
6
12
,
5
3
6
,
±
1
2
)
{\displaystyle \left({\frac {\sqrt {10}}{20}},\,{\frac {5{\sqrt {6}}}{12}},\,{\frac {5{\sqrt {3}}}{6}},\,\pm {\frac {1}{2}}\right)}
(
10
20
,
−
7
6
12
,
3
3
,
±
1
)
{\displaystyle \left({\frac {\sqrt {10}}{20}},\,-{\frac {7{\sqrt {6}}}{12}},\,{\frac {\sqrt {3}}{3}},\,\pm 1\right)}
(
10
20
,
−
7
6
12
,
−
2
3
3
,
0
)
{\displaystyle \left({\frac {\sqrt {10}}{20}},\,-{\frac {7{\sqrt {6}}}{12}},\,-{\frac {2{\sqrt {3}}}{3}},\,0\right)}
(
−
10
5
,
0
,
3
2
,
±
3
2
)
{\displaystyle \left(-{\frac {\sqrt {10}}{5}},\,0,\,{\frac {\sqrt {3}}{2}},\,\pm {\frac {3}{2}}\right)}
(
−
10
5
,
0
,
−
3
,
0
)
{\displaystyle \left(-{\frac {\sqrt {10}}{5}},\,0,\,-{\sqrt {3}},\,0\right)}
(
−
10
5
,
6
3
,
3
6
,
±
3
2
)
{\displaystyle \left(-{\frac {\sqrt {10}}{5}},\,{\frac {\sqrt {6}}{3}},\,{\frac {\sqrt {3}}{6}},\,\pm {\frac {3}{2}}\right)}
(
−
10
5
,
6
3
,
2
3
3
,
±
1
)
{\displaystyle \left(-{\frac {\sqrt {10}}{5}},\,{\frac {\sqrt {6}}{3}},\,{\frac {2{\sqrt {3}}}{3}},\,\pm 1\right)}
(
−
10
5
,
6
3
,
−
5
3
6
,
±
1
2
)
{\displaystyle \left(-{\frac {\sqrt {10}}{5}},\,{\frac {\sqrt {6}}{3}},\,-{\frac {5{\sqrt {3}}}{6}},\,\pm {\frac {1}{2}}\right)}
(
−
10
5
,
−
2
6
3
,
3
6
,
±
1
2
)
{\displaystyle \left(-{\frac {\sqrt {10}}{5}},\,-{\frac {2{\sqrt {6}}}{3}},\,{\frac {\sqrt {3}}{6}},\,\pm {\frac {1}{2}}\right)}
(
−
10
5
,
−
2
6
3
,
−
3
3
,
0
)
{\displaystyle \left(-{\frac {\sqrt {10}}{5}},\,-{\frac {2{\sqrt {6}}}{3}},\,-{\frac {\sqrt {3}}{3}},\,0\right)}
(
3
10
10
,
−
6
6
,
3
6
,
±
3
2
)
{\displaystyle \left({\frac {3{\sqrt {10}}}{10}},\,-{\frac {\sqrt {6}}{6}},\,{\frac {\sqrt {3}}{6}},\,\pm {\frac {3}{2}}\right)}
(
3
10
10
,
6
6
,
−
3
6
,
±
3
2
)
{\displaystyle \left({\frac {3{\sqrt {10}}}{10}},\,{\frac {\sqrt {6}}{6}},\,-{\frac {\sqrt {3}}{6}},\,\pm {\frac {3}{2}}\right)}
(
3
10
10
,
−
6
6
,
2
3
3
,
±
1
)
{\displaystyle \left({\frac {3{\sqrt {10}}}{10}},\,-{\frac {\sqrt {6}}{6}},\,{\frac {2{\sqrt {3}}}{3}},\,\pm 1\right)}
(
3
10
10
,
6
6
,
−
2
3
3
,
±
1
)
{\displaystyle \left({\frac {3{\sqrt {10}}}{10}},\,{\frac {\sqrt {6}}{6}},\,-{\frac {2{\sqrt {3}}}{3}},\,\pm 1\right)}
(
3
10
10
,
−
6
6
,
−
5
3
6
,
±
1
2
)
{\displaystyle \left({\frac {3{\sqrt {10}}}{10}},\,-{\frac {\sqrt {6}}{6}},\,-{\frac {5{\sqrt {3}}}{6}},\,\pm {\frac {1}{2}}\right)}
(
3
10
10
,
6
6
,
5
3
6
,
±
1
2
)
{\displaystyle \left({\frac {3{\sqrt {10}}}{10}},\,{\frac {\sqrt {6}}{6}},\,{\frac {5{\sqrt {3}}}{6}},\,\pm {\frac {1}{2}}\right)}
(
3
10
10
,
±
6
2
,
0
,
±
1
)
{\displaystyle \left({\frac {3{\sqrt {10}}}{10}},\,\pm {\frac {\sqrt {6}}{2}},\,0,\,\pm 1\right)}
(
3
10
10
,
±
6
2
,
±
3
2
,
±
1
2
)
{\displaystyle \left({\frac {3{\sqrt {10}}}{10}},\,\pm {\frac {\sqrt {6}}{2}},\,\pm {\frac {\sqrt {3}}{2}},\,\pm {\frac {1}{2}}\right)}
(
−
9
10
20
,
−
6
12
,
3
3
,
±
1
)
{\displaystyle \left(-{\frac {9{\sqrt {10}}}{20}},\,-{\frac {\sqrt {6}}{12}},\,{\frac {\sqrt {3}}{3}},\,\pm 1\right)}
(
−
9
10
20
,
−
6
12
,
−
2
3
3
,
0
)
{\displaystyle \left(-{\frac {9{\sqrt {10}}}{20}},\,-{\frac {\sqrt {6}}{12}},\,-{\frac {2{\sqrt {3}}}{3}},\,0\right)}
(
−
9
10
20
,
6
4
,
0
,
±
1
)
{\displaystyle \left(-{\frac {9{\sqrt {10}}}{20}},\,{\frac {\sqrt {6}}{4}},\,0,\,\pm 1\right)}
(
−
9
10
20
,
6
4
,
±
3
2
,
±
1
2
)
{\displaystyle \left(-{\frac {9{\sqrt {10}}}{20}},\,{\frac {\sqrt {6}}{4}},\,\pm {\frac {\sqrt {3}}{2}},\,\pm {\frac {1}{2}}\right)}
(
−
9
10
20
,
−
5
6
12
,
3
6
,
±
1
2
)
{\displaystyle \left(-{\frac {9{\sqrt {10}}}{20}},\,-{\frac {5{\sqrt {6}}}{12}},\,{\frac {\sqrt {3}}{6}},\,\pm {\frac {1}{2}}\right)}
(
−
9
10
20
,
−
5
6
12
,
−
3
3
,
0
)
{\displaystyle \left(-{\frac {9{\sqrt {10}}}{20}},\,-{\frac {5{\sqrt {6}}}{12}},\,-{\frac {\sqrt {3}}{3}},\,0\right)}
Much simpler coordinates can be given in five dimensions , as all permutations of:
(
3
2
2
,
2
,
2
2
,
0
,
0
)
{\displaystyle \left({\frac {3{\sqrt {2}}}{2}},\,{\sqrt {2}},\,{\frac {\sqrt {2}}{2}},\,0,\,0\right)}
The great rhombated pentachoron has the following Coxeter diagrams :
x3x3x3o ( (full symmetry)
xuxx3xxux3ooox&#xt (A3 axial, truncated tetrahedron-first)
xu(xd)uxo xu(dx)uxx3oo(ox)xux&#xt (A2 ×A1 symmetry, triangular prism-first) The great rhombated pentachoron has a semi-uniform variant of the form x3y3z3o that maintains its full symmetry. This variant uses 5 semi-uniform truncated tetrahedra of form y3z3o, 5 great rhombitetratetrahedra of form x3y3z, and 10 triangular prisms of form x z3o as cells, with 3 edge lengths.
With edges of lengths a, b, and c (such that it is given by a3b3c3o), its circumradius is given by
2
a
2
+
3
b
2
+
3
c
2
+
3
a
b
+
2
a
c
+
4
b
c
5
{\displaystyle {\sqrt {\frac {2a^{2}+3b^{2}+3c^{2}+3ab+2ac+4bc}{5}}}}
Uniform polychoron compounds composed of great rhombated pentachora include:
Name OBSA Schläfli symbol CD diagram Image Pentachoron pen {3,3,3} Rectified pentachoron rap r{3,3,3} Rectified pentachoron rap r{3,3,3} Pentachoron pen {3,3,3} Truncated pentachoron tip t{3,3,3} Small rhombated pentachoron srip rr{3,3,3} Small prismatodecachoron spid t0,3 {3,3,3} Decachoron deca 2t{3,3,3} Small rhombated pentachoron srip rr{3,3,3} Truncated pentachoron tip t{3,3,3} Great rhombated pentachoron grip tr{3,3,3} Prismatorhombated pentachoron prip t0,1,3 {3,3,3} Prismatorhombated pentachoron prip t0,2,3 {3,3,3} Great rhombated pentachoron grip tr{3,3,3} Great prismatodecachoron gippid t0,1,2,3 {3,3,3}







 ) (full symmetry)
) (full symmetry)