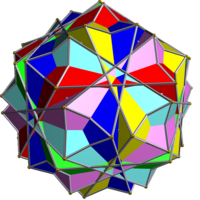
Compound of six pentagonal antiprisms
(Redirected from Great snub dodecahedron)
| Compound of six pentagonal antiprisms | |
|---|---|
 | |
| Rank | 3 |
| Type | Uniform |
| Notation | |
| Bowers style acronym | Gassid |
| Elements | |
| Components | 6 pentagonal antiprisms |
| Faces | 60 triangles, 12 pentagons |
| Edges | 60+60 |
| Vertices | 60 |
| Vertex figure | Isosceles trapezoid, edge length 1, 1, 1, (1+√5)/2 |
| Measures (edge length 1) | |
| Circumradius | |
| Volume | |
| Dihedral angles | 3–3: |
| 5–3: | |
| Central density | 6 |
| Number of external pieces | 600 |
| Level of complexity | 33 |
| Related polytopes | |
| Army | Semi-uniform Tid, edge lengths (triangles) and (between dipentagons) |
| Regiment | Gassid |
| Dual | Compound of six pentagonal antitegums |
| Conjugate | Compound of six pentagrammic retroprisms |
| Convex hull | Semi-uniform Tid |
| Convex core | Dodecahedron |
| Abstract & topological properties | |
| Flag count | 480 |
| Orientable | Yes |
| Properties | |
| Symmetry | H3, order 120 |
| Convex | No |
| Nature | Tame |
The great snub dodecahedron, gassid, or compound of six pentagonal antiprisms is a uniform polyhedron compound. It consists of 60 triangles and 12 pentagons, with one pentagon and three triangles joining at a vertex.
This compound can be formed by inscribing six pentagonal antiprisms within an icosahedron (each by removing one pair of opposite vertices) and then rotating each antiprism by 36º around its axis.
Its quotient prismatic equivalent is the pentagonal antiprismatic hexateroorthowedge, which is eight-dimensional.
A double cover of this compound occurs as a special case of the great disnub dodecahedron.
Vertex coordinates[edit | edit source]
Coordinates for the vertices of a great snub dodecahedron of edge length 1 are given by all even permutations of:
External links[edit | edit source]
- Bowers, Jonathan. "Polyhedron Category C8: Antiprismatics" (#48).
- Klitzing, Richard. "gassid".
- Wikipedia contributors. "Compound of six pentagonal antiprisms".








