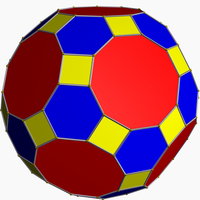
Great rhombicosidodecahedron

Great rhombicosidodecahedron
(3D model) (OFF file)
Rank	3
Type	Uniform
Space	Spherical
Notation
Bowers style acronym	Grid
Coxeter diagram	x5x3x ()
Elements
Faces	30 squares, 20 hexagons, 12 decagons
Edges	60+60+60
Vertices	120
Vertex figure	Scalene triangle, edge lengths √2, √3, √(5+√5)/2
Measures (edge length 1)
Circumradius	$\frac{\sqrt{31+12\sqrt5}}{2} ≈ 3.80239$
Volume	$5(19+10\sqrt5) ≈ 206.80340$
Dihedral angles	6–4: $\arccos\left(-\frac{\sqrt3+\sqrt{15}}{6}\right) ≈ 159.09484^\circ$
	10–4: $\arccos\left(-\sqrt{\frac{5+\sqrt5}{10}}\right) ≈ 148.28253^\circ$
	10–6: $\arccos\left(-\sqrt{\frac{5+2\sqrt5}{15}}\right) ≈ 142.62263^\circ$
Central density	1
Number of external pieces	62
Level of complexity	6
Related polytopes
Army	Grid
Regiment	Grid
Dual	Disdyakis triacontahedron
Conjugate	Great quasitruncated icosidodecahedron
Abstract & topological properties
Flag count	720
Euler characteristic	2
Surface	Sphere
Orientable	Yes
Genus	0
Properties
Symmetry	H3, order 120
Convex	Yes
Nature	Tame

For the nonconvex conjugate of the small rhombicosidodecahedron, see quasirhombicosidodecahedron.

The great rhombicosidodecahedron or grid, also commonly known as the truncated icosidodecahedron, is the most complex of the 13 Archimedean solids. It consists of 12 decagons, 20 hexagons, and 30 squares, with one of each type of face meeting per vertex. It can be obtained by cantitruncation of the dodecahedron or icosahedron, or equivalently by truncating the vertices of an icosidodecahedron and then adjusting the edge lengths to be all equal.

This is one of three Wythoffian non-prismatic polyhedra whose Coxeter diagram nodes are all ringed, the other two being the great rhombitetratetrahedron and the great rhombicuboctahedron.

It can be alternated into the snub dodecahedron after edge lengths are equalized.

Vertex coordinates

A great rhombicosidodecahedron of edge length 1 has vertex coordinates given by all permutations of

• $\left(±\frac12,\,±\frac12,\,±\frac{3+2\sqrt5}{2}\right),$

along with all even permutations of:

• $\left(±\frac12,\,±\frac{2+\sqrt5}{2},\,±\frac{4+\sqrt5}{2}\right),$
• $\left(±1,\,±\frac{3+\sqrt5}{4},\,±\frac{7+3\sqrt5}{4}\right),$
• $\left(±\frac{3+\sqrt5}{4},\,±3\frac{1+\sqrt5}{4},\,±\frac{3+\sqrt5}{2}\right),$
• $\left(±\frac{1+\sqrt5}{2},\,±\frac{5+3\sqrt5}{4},\,±\frac{5+\sqrt5}{4}\right).$

Representations

A great rhombicosidodecahedron has the following Coxeter diagrams:

• x5x3x (full symmetry)
• xuxxuAxFVFxx5xxFVFxAuxxux&#xt (H2 axial, decagon-first)

Semi-uniform variant

The great rhombicosidodecahedron has a semi-uniform variant of the form x5y3z that maintains its full symmetry. This variant has 12 dipentagons, 20 ditrigons, and 30 rectangles as faces.

With edges of length a (dipentagon-rectangle), b (dipentagon-ditrigon), and c (ditrigon-rectangle), its circumradius is given by $\sqrt{\frac{9a^2+12b^2+5c^2+16ab+8ac+12bc+(3a^2+4b^2+c^2+8ab+4ac+4bc)\sqrt5}{8}}$ and its volume is given by $\frac{15a^3+60a^2b+45a^2c+60ab^2+60abc+15ac^2+30b^3+60b^2c+30bc^2+5c^3}{4}+(21a^3+72a^2b+45a^2c+108ab^2+180abc+45ac^2+34b^3+60b^2c+30bc^2+5c^3)\frac{\sqrt5}{12}$.

Related polyhedra

o5o3o truncations

Name	OBSA	Schläfli symbol	CD diagram	Picture
Dodecahedron	doe	{5,3}	x5o3o
Truncated dodecahedron	tid	t{5,3}	x5x3o
Icosidodecahedron	id	r{5,3}	o5x3o
Truncated icosahedron	ti	t{3,5}	o5x3x
Icosahedron	ike	{3,5}	o5o3x
Small rhombicosidodecahedron	srid	rr{5,3}	x5o3x
Great rhombicosidodecahedron	grid	tr{5,3}	x5x3x
Snub dodecahedron	snid	sr{5,3}	s5s3s

External links

• Bowers, Jonathan. "Polyhedron Category 5: Omnitruncates" (#58).

• Klitzing, Richard. "grid".

• Quickfur. "The Great Rhombicosidodecahedron".

• Wikipedia Contributors. "Truncated icosidodecahedron".
• McCooey, David. "Truncated Icosidodecahedron"

• Hi.gher.Space Wiki Contributors. "Rhodopantohedron".