Heptagonal prism

Heptagonal prism
(3D model) (OFF file)
Rank	3
Type	Uniform
Notation
Bowers style acronym	Hep
Coxeter diagram	x x7o ()
Conway notation	P7
Elements
Faces	7 squares, 2 heptagons
Edges	7+14
Vertices	14
Vertex figure	Isosceles triangle, edge lengths √2, √2, 2cos(π/7)
Measures (edge length 1)
Circumradius	${\frac {\sqrt {1+{\frac {1}{\sin ^{2}{\frac {\pi }{7}}}}}}{2}}\approx 1.25618$
Volume	${\frac {7}{4\tan {\frac {\pi }{7}}}}\approx 3.63391$
Dihedral angles	4–4: ${\frac {5\pi }{7}}\approx 128.57143^{\circ }$
	4–7: 90°
Height	1
Central density	1
Number of external pieces	9
Level of complexity	3
Related polytopes
Army	Hep
Regiment	Hep
Dual	Heptagonal tegum
Conjugates	Heptagrammic prism, Great heptagrammic prism
Abstract & topological properties
Flag count	84
Euler characteristic	2
Surface	Sphere
Orientable	Yes
Genus	0
Skeleton	GP(7,1)
Properties
Symmetry	I2(7)×A1, order 28
Convex	Yes
Nature	Tame

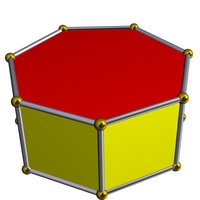
The heptagonal prism, or hep, is a prismatic uniform polyhedron. It consists of 2 heptagons and 7 squares. Each vertex joins one heptagon and two squares. As the name suggests, it is a prism based on a heptagon.

Vertex coordinates

The coordinates of a heptagonal prism, centered at the origin and with edge length 2sin(π/7), are given by:

• $\left(1,\,0,\,\pm \sin {\frac {\pi }{7}}\right)$,
• $\left(\cos \left({\frac {2\pi }{7}}\right),\,\pm \sin \left({\frac {2\pi }{7}}\right),\,\pm \sin {\frac {\pi }{7}}\right)$,
• $\left(\cos \left({\frac {4\pi }{7}}\right),\,\pm \sin \left({\frac {4\pi }{7}}\right),\,\pm \sin {\frac {\pi }{7}}\right)$,
• $\left(\cos \left({\frac {6\pi }{7}}\right),\,\pm \sin \left({\frac {6\pi }{7}}\right),\,\pm \sin {\frac {\pi }{7}}\right)$.

External links

• Klitzing, Richard. "hep".
• Quickfur. "The Heptagonal Prism".

• Wikipedia contributors. "Heptagonal prism".
• McCooey, David. "Heptagonal Prism"