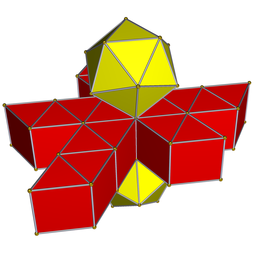
Icosahedral prism

Icosahedral prism
(OFF file)
Rank	4
Type	Uniform
Space	Spherical
Notation
Bowers style acronym	Ipe
Coxeter diagram	x o5o3x ()
Elements
Cells	20 triangular prisms, 2 icosahedra
Faces	40 triangles, 30 squares
Edges	12+60
Vertices	24
Vertex figure	Pentagonal pyramid, edge lengths 1 (base), √2 (legs)
Measures (edge length 1)
Circumradius	$\sqrt{\frac{7+\sqrt5}{8}} ≈ 1.07448$
Hypervolume	$5\frac{3+\sqrt5}{12} ≈ 2.18169$
Dichoral angles	Trip–4–trip: $\arccos\left(-\frac{\sqrt5}{3}\right) ≈ 138.18969°$
	Ike–3–trip: 90°
Height	1
Central density	1
Number of external pieces	22
Level of complexity	4
Related polytopes
Army	Ipe
Regiment	Ipe
Dual	Dodecahedral tegum
Conjugate	Great icosahedral prism
Abstract & topological properties
Flag count	960
Euler characteristic	0
Orientable	Yes
Properties
Symmetry	H3×A1, order 240
Convex	Yes
Nature	Tame

The icosahedral prism or ipe is a prismatic uniform polychoron that consists of 2 icosahedra and 20 triangular prisms. Each vertex joins 1 icosahedron and 5 triangular prisms. It is a prism based on the icosahedron. As such it is also a convex segmentochoron (designated K-4.36 in Richard Klitzing's list).

Gallery

• 

  Card with cell counts, verf, and cross-sections

• 

  Segmentochoron display, ike atop ike

• 

  Net

Vertex coordinates

The vertices of an icosahedral prism of edge length 1 are given by all even permutations and all sign changes of the first three coordinates of:

• $\left(0,\,±\frac12,\,±\frac{1+\sqrt5}{4},\,±\frac12\right).$

Representations

An icosahedral prism has the following Coxeter diagrams:

• x o5o3x (full symmetry)
• x2s3s4o () (bases as pyritohedral symmetry)
• x2s3s3s () (as snub tetrahedral prism)
• oo5oo3xx&#x (bases seen separately)
• xxxx oxoo5ooxo&#xt (H₂×A₁ axial, edge-first)

Related polychora

An icosahedral prism can be cut into a central pentagonal antiprismatic prism augmented with 2 pentagonal pyramidal prisms.

The regiment of the icosahedral prism also contains the great dodecahedral prism.

External links

• Bowers, Jonathan. "Category 19: Prisms" (#892).

• Klitzing, Richard. "Ipe".

• Wikipedia Contributors. "Icosahedral prism".