Order-∞ square tiling

Order-∞ square tiling
Rank	3
Type	Regular, paracompact
Space	Hyperbolic
Notation
Bowers style acronym	Asquat
Coxeter diagram	o∞o4x ()
Schläfli symbol	{4,∞}
Elements
Faces	NM squares
Edges	2NM
Vertices	4N
Vertex figure	Apeirogon, edge length √2
Measures (edge length 1)
Circumradius
Related polytopes
Army	Asquat
Regiment	Asquat
Dual	Order-4 apeirogonal tiling
Topological properties
Surface	Sphere
Orientable	Yes
Genus	0
Properties
Symmetry	[∞,4]
Convex	Yes

The order-∞ square tiling or infinite-order square tiling is a paracompact regular tiling of the hyperbolic plane. Infinitely many ideal squares join at each vertex. All vertices are ideal points at infinity.

The tiling can be alternated to produce the order-∞ apeirogonal tiling.

Representations[edit | edit source]

An order–∞ square tiling has the following Coxeter diagrams:

o∞o4x (full symmetry)
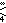
o4x4o∞*a (squares of two types)

Related polytopes[edit | edit source]

o∞o4o truncations
Name	OBSA	Schläfli symbol
Order-4 apeirogonal tiling	squazat	{∞,4}
Truncated order-4 apeirogonal tiling	tosquazat	t{∞,4}
Tetraapeirogonal tiling	tezt	r{∞,4}
Truncated order-∞ square tiling	tazsquat	t{4,∞}
Order-∞ square tiling	azsquat	{4,∞}
Small rhombitetraapeirogonal tiling	srotezt	rr{∞,4}
Great rhombitetraapeirogonal tiling	grotezt	tr{∞,4}
Snub tetraapeirogonal tiling		sr{∞,4}