Order-4 hexagonal tiling honeycomb
Jump to navigation
Jump to search
| Order-4 hexagonal tiling honeycomb | |
|---|---|
 | |
| Rank | 4 |
| Type | Regular, paracompact |
| Space | Hyperbolic |
| Notation | |
| Bowers style acronym | Shexah |
| Coxeter diagram | x6o3o4o (     ) |
| Schläfli symbol | {6,3,4} |
| Elements | |
| Cells | 4N hexagonal tilings |
| Faces | 2NM hexagons |
| Edges | 3NM |
| Vertices | NM |
| Vertex figure | Octahedron, edge length √3 |
| Measures (edge length 1) | |
| Circumradius | |
| Related polytopes | |
| Army | Shexah |
| Regiment | Shexah |
| Dual | Order-6 cubic honeycomb |
| Petrie dual | Petrial order-4 hexagonal tiling honeycomb |
| Abstract & topological properties | |
| Orientable | Yes |
| Properties | |
| Symmetry | [6,3,4] |
| Convex | Yes |
The order-4 hexagonal tiling honeycomb is a paracompact regular tiling of 3D hyperbolic space. Each cell is a hexagonal tiling whose vertices lie on a horosphere, a surface in hyperbolic space that approaches a single ideal point at infinity. 4 hexagonal tilings meet at each edge, and 8 meet at each vertex.
Representations[edit | edit source]
An order-4 hexagonal tiling has the following Coxeter diagrams:
- x6o3o4o () (full symmetry)
- o3o6x *b3o (
) (half symmetry, 2 types of cells) - x3x6o3o6*a (
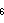
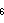) (has a triangular antiprism verf)
Related polytopes[edit | edit source]
The hexagonal faces of the order-4 hexagonal tiling honeycomb form the regular skew polyhedron {6,6∣6}.
External links[edit | edit source]
- Klitzing, Richard. "shexah".
- Wikipedia contributors. "Order-4 hexagonal tiling honeycomb".
- lllllllllwith10ls. "Category 1: Regulars" (#7).
| truncations | ||||
|---|---|---|---|---|
| Name | OBSA | Schläfli symbol | CD diagram | Image |
| Order-4 hexagonal tiling honeycomb | shexah | {6,3,4} | | |
| Truncated order-4 hexagonal tiling honeycomb | tishexah | t{6,3,4} | |  |
| Rectified order-4 hexagonal tiling honeycomb | rishexah | r{6,3,4} | |  |
| Cubic-hexagonal tiling honeycomb | chexah | 2t{6,3,4} | |  |
| Rectified order-6 cubic honeycomb | rihach | r{4,3,6} | |  |
| Truncated order-6 cubic honeycomb | thach | t{4,3,6} | |  |
| Order-6 cubic honeycomb | hachon | {4,3,6} | |  |
| Small rhombated order-4 hexagonal tiling honeycomb | srishexah | rr{6,3,4} | |  |
| Great rhombated order-4 hexagonal tiling honeycomb | grishexah | tr{6,3,4} | |  |
| Small rhombated order-6 cubic honeycomb | srihach | rr{4,3,6} | |  |
| Great rhombated order-6 cubic honeycomb | grihach | tr{4,3,6} | |  |
| Small prismated order-4 hexagonal tiling honeycomb | sidpichexah | t0,3{6,3,4} | |  |
| Prismatorhombated order-6 cubic honeycomb | prihach | t0,1,3{6,3,4} | |  |
| Prismatorhombated order-4 hexagonal tiling honeycomb | prishexah | t0,1,3{4,3,6} | |  |
| Great prismated order-4 hexagonal tiling honeycomb | gidpichexah | t0,1,2,3{6,3,4} | |  |