Pentagonal antiprism

Pentagonal antiprism
(3D model) (OFF file)
Rank	3
Type	Uniform
Notation
Bowers style acronym	Pap
Coxeter diagram	s2s10o ()
Conway notation	A5
Elements
Faces	10 triangles, 2 pentagons
Edges	10+10
Vertices	10
Vertex figure	Isosceles trapezoid, edge lengths 1, 1, 1, (1+√5)/2
Measures (edge length 1)
Circumradius	${\sqrt {\frac {5+{\sqrt {5}}}{8}}}\approx 0.95106$
Volume	${\frac {5+2{\sqrt {5}}}{6}}\approx 1.57869$
Dihedral angles	3–3: $\arccos \left(-{\frac {\sqrt {5}}{3}}\right)\approx 138.18969^{\circ }$
	5–3: $\arccos \left(-{\sqrt {\frac {5-2{\sqrt {5}}}{15}}}\right)\approx 100.81232^{\circ }$
Height	${\sqrt {\frac {5+{\sqrt {5}}}{10}}}\approx 0.85065$
Central density	1
Number of external pieces	12
Level of complexity	4
Related polytopes
Army	Pap
Regiment	Pap
Dual	Pentagonal antitegum
Conjugate	Pentagrammic retroprism
Abstract & topological properties
Flag count	80
Euler characteristic	2
Surface	Sphere
Orientable	Yes
Genus	0
Properties
Symmetry	(I2(10)×A1)/2, order 20
Convex	Yes
Nature	Tame

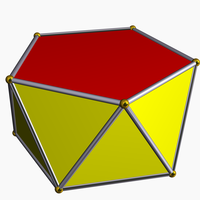
The pentagonal antiprism, or pap, is a prismatic uniform polyhedron. It consists of 10 triangles and 2 pentagons. Each vertex joins one pentagon and three triangles. As the name suggests, it is an antiprism based on a pentagon.

It can also be obtained as a diminishing of the regular icosahedron when two pentagonal pyramids are removed from opposite ends.

Vertex coordinates

A pentagonal antiprism of edge length 1 has vertex coordinates given by:

• $\left(\pm {\frac {1+{\sqrt {5}}}{4}},\,\pm {\frac {1}{2}},\,0\right),$
• $\left(0,\,\pm {\frac {1+{\sqrt {5}}}{4}},\,\pm {\frac {1}{2}}\right),$
• $\pm \left({\frac {1}{2}},\,0,\,{\frac {1+{\sqrt {5}}}{4}}\right).$

These coordinates are obtained by removing two opposite vertices from a regular icosahedron.

An alternative set of coordinates can be constructed in a similar way to other polygonal antiprisms, giving the vertices as the following points:

• $\pm \left(\pm {\frac {1}{2}},\,-{\sqrt {\frac {5+2{\sqrt {5}}}{20}}},\,{\sqrt {\frac {5+{\sqrt {5}}}{40}}}\right),$
• $\pm \left(\pm {\frac {1+{\sqrt {5}}}{4}},\,{\sqrt {\frac {5-{\sqrt {5}}}{40}}},\,{\sqrt {\frac {5+{\sqrt {5}}}{40}}}\right),$
• $\pm \left(0,\,{\sqrt {\frac {5+{\sqrt {5}}}{10}}},\,{\sqrt {\frac {5+{\sqrt {5}}}{40}}}\right).$

Representations

A pentagonal antiprism has the following Coxeter diagrams:

• s2s10o (alternated decagonal prism)
• s2s5s (alternated dipentagonal prism)
• xo5ox&#x (bases considered separately)

General variant

The pentagonal antiprism has a general isogonal variant of the form xo5ox&#y that maintains its full symmetry. This variant uses isosceles triangles as sides.

If the base edges are of length b and the lacing edges are of length l, its height is given by ${\sqrt {l^{2}-b^{2}{\frac {5-{\sqrt {5}}}{10}}}}$.

The bases of the pentagonal antiprism are rotated from each other by an angle of 36°. If this angle is changed the result is more properly called a pentagonal gyroprism.

A notable case occurs as the alternation of the uniform decagonal prism. This specific case has base edges of length ${\sqrt {\frac {5+{\sqrt {5}}}{2}}}$ and side edges of length ${\sqrt {2}}$.

Related polyhedra

A pentagonal pyramid can be attached to a base of the pentagonal antiprism to form the gyroelongated pentagonal pyramid. If a second pyramid is attached to the other base, the result is the gyroelongated pentagonal bipyramid, better known as the regular icosahedron.

Two non-prismatic uniform polyhedron compounds are composed of pentagonal antiprisms:

• Great snub dodecahedron (6)
• Great disnub dodecahedron (12)

There are also an infinite amount of prismatic uniform compounds that are the antiprisms of compounds of pentagons.

External links

• Bowers, Jonathan. "Batch 2: Ike and Sissid Facetings" (#3 under ike).

• Klitzing, Richard. "pap".

• Quickfur. "The Pentagonal Antiprism".

• Wikipedia Contributors. "Pentagonal antiprism".
• McCooey, David. "Pentagonal Antiprism"