Rectified pentachoron

Rectified pentachoron
(OFF file)
Rank	4
Type	Uniform
Space	Spherical
Notation
Bowers style acronym	Rap
Coxeter diagram	o3x3o3o ()
Elements
Cells	5 tetrahedra, 5 octahedra
Faces	10+20 triangles
Edges	30
Vertices	10
Vertex figure	Triangular prism, edge length 1
Edge figure	tet 3 oct 3 oct 3
Measures (edge length 1)
Circumradius	$\frac{\sqrt{15}}{5} ≈ 0.77460$
Hypervolume	$\frac{11\sqrt5}{96} ≈ 0.25622$
Dichoral angles	Oct–3–tet: $\arccos\left(-\frac14\right) ≈ 104.47751^\circ$
	Oct-3-oct: $\arccos\left(\frac14\right) ≈ 75.52249^\circ$
Height	$\frac{\sqrt{10}}{4} ≈ 0.79057$
Central density	1
Number of external pieces	10
Level of complexity	3
Related polytopes
Army	Rap
Regiment	Rap
Dual	Joined pentachoron
Conjugate	None
Abstract & topological properties
Flag count	360
Euler characteristic	0
Orientable	Yes
Properties
Symmetry	A4, order 120
Convex	Yes
Nature	Tame

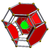
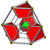
The rectified pentachoron, or rap, also commonly called the rectified 5-cell, is a convex uniform polychoron that consists of 5 regular tetrahedra and 5 regular octahedra. Two tetrahedra and three octahedra join at each triangular prismatic vertex. As the name suggests, it can be constructed by rectification of the pentachoron.

It is the vertex figure of the demipenteract.

It is also a convex segmentochoron (designated K-4.5 in Richard Klitzing's list), formed as a tetrahedron atop an octahedron. If the edge lengths of this subsymmetrical variation are changed, the result is various non-uniform tetrahedron atop octahedron polychora with 4 triangle antipodiums and 4 triangle pyramids as sides.

It is also isogonal under the 5-2 step prism subsymmetry, and can be considered to be a 5-2 double step prism.

Gallery

Vertex coordinates

The vertices of a rectified pentachoron of edge length 1 are given by:

• $\left(-\frac{3\sqrt{10}}{20},\,-\frac{\sqrt6}{4},\,0,\,0\right),$
• $\left(-\frac{3\sqrt{10}}{20},\,\frac{\sqrt6}{12},\,-\frac{\sqrt3}{3},\,0\right),$
• $\left(-\frac{3\sqrt{10}}{20},\,\frac{\sqrt6}{12},\,\frac{\sqrt3}{6},\,±\frac12\right),$
• $\left(\frac{\sqrt{10}}{10},\,\frac{\sqrt6}{6},\,\frac{\sqrt3}{3},\,0\right),$
• $\left(\frac{\sqrt{10}}{10},\,-\frac{\sqrt6}{6},\,-\frac{\sqrt3}{3},\,0\right),$
• $\left(\frac{\sqrt{10}}{10},\,\frac{\sqrt6}{6},\,-\frac{\sqrt3}{6},\,±\frac12\right),$
• $\left(\frac{\sqrt{10}}{10},\,-\frac{\sqrt6}{6},\,\frac{\sqrt3}{6},\,±\frac12\right).$

Simpler coordinates can be given by all even sign changes of first 3 coordinates of:

• $\left(\frac{\sqrt2}{4},\,\frac{\sqrt2}{4},\,\frac{\sqrt2}{4},\,\frac{3\sqrt{10}}{20}\right),$

and all permutations of the first three coordinates of:

• $\left(±\frac{\sqrt2}{2},\,0,\,0,\,-\frac{\sqrt{10}}{10}\right).$

Much simpler coordinates can be given in five dimensions, as all permutations of:

• $\left(\frac{\sqrt2}{2},\,\frac{\sqrt2}{2},\,0,\,0,\,0\right).$

Representations

A rectified pentachoron has the following Coxeter diagrams:

• o3x3o3o (full symmetry)
• xo3ox3oo&#x (A3 axial, as tetrahedron atop octahedron
• oxo oxo3oox&#xt (A2×A1 axial, vertex-first)
• oxoo3xoxo&#xr (A2 axial)
• oxoox oxoxo&#xr (A1×A1 axial)

Segmentochoron display

• 

  Tetrahedron atop octahedron

Related polychora

The rectified pentachoron is the colonel of a three-member regiment that also includes the facetorectified pentachoron and the prismatointercepted pentachoron.

The rectified pentachoron can be diminished by cutting off triangular prismatic pyramids, with each removing 2 tetrahedra and diminishing the octahedra down to square pyramids. If one pyramid is removed, the result is the triangular antifastegium. If two non-adjacent pyramids are removed, such that one of the octahedra gets reduced down to an equatorial square only, the result is the bidiminished rectified pentachoron.

An octahedral pyramid can be attached to one of the rectified pentachoron's octahedral cells to create the augmented rectified pentachoron, notable as a non-uniform Blind polytope.

Uniform polychoron compounds composed of rectified pentachora include:

• Rectified stellated decachoron (2)
• Compound of 12 rectified pentachora (12)
• Rectified medial hexacosichoron (120)

o3o3o3o truncations

Name	OBSA	CD diagram	Picture
Pentachoron	pen	x3o3o3o ()
Truncated pentachoron	tip	x3x3o3o ()
Rectified pentachoron	rap	o3x3o3o ()
Decachoron	deca	o3x3x3o ()
Rectified pentachoron	rap	o3o3x3o ()
Truncated pentachoron	tip	o3o3x3x ()
Pentachoron	pen	o3o3o3x ()
Small rhombated pentachoron	srip	x3o3x3o ()
Great rhombated pentachoron	grip	x3x3x3o ()
Small rhombated pentachoron	srip	o3x3o3x ()
Great rhombated pentachoron	grip	o3x3x3x ()
Small prismatodecachoron	spid	x3o3o3x ()
Prismatorhombated pentachoron	prip	x3x3o3x ()
Prismatorhombated pentachoron	prip	x3o3x3x ()
Great prismatodecachoron	gippid	x3x3x3x ()

Isogonal derivatives

Substitution by vertices of these following elements will produce these convex isogonal polychora:

• Octahedron (5): Pentachoron
• Tetrahedron (5): Pentachoron
• Triangle (10): Rectified pentachoron
• Triangle (20): Semi-uniform small prismatodecachoron without doubled symmetry
• Edge (30): Uniform small rhombated pentachoron

External links

• Bowers, Jonathan. "Category 3: Triangular Rectates" (#39).

• Bowers, Jonathan. "Pennic and Decaic Isogonals".

• Klitzing, Richard. "rap".

• Quickfur. "The Rectified 5-cell".

• Wikipedia Contributors. "Rectified 5-cell".
• Hi.gher.Space Wiki Contributors. "Pyrorectichoron".