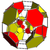
Rectified tesseract

Rectified tesseract
(OFF file)
Rank	4
Type	Uniform
Space	Spherical
Notation
Bowers style acronym	Rit
Coxeter diagram	o4x3o3o ()
Elements
Cells	16 tetrahedra, 8 cuboctahedra
Faces	64 triangles, 24 squares
Edges	96
Vertices	32
Vertex figure	Semi-uniform triangular prism, edge lengths 1 (base) and √2 (side)
Edge figure	tet 3 co 4 co 3
Measures (edge length 1)
Circumradius	$\frac{\sqrt6}{2} \approx 1.224744871$
Hypervolume	$\frac{23}{6} \approx 3.833333333$
Dichoral angles	Co–3–tet: 120°
	Co–4–co: 90°
Central density	1
Number of external pieces	24
Level of complexity	3
Related polytopes
Army	Rit
Regiment	Rit
Dual	Joined hexadecachoron
Conjugate	None
Abstract & topological properties
Flag count	1152
Euler characteristic	0
Orientable	Yes
Properties
Symmetry	B4, order 384
Convex	Yes
Nature	Tame

The rectified tesseract, or rit, is a convex uniform polychoron that consists of 16 regular tetrahedra and 8 cuboctahedra. Two tetrahedra and three cuboctahedra join at each triangular prismatic vertex. As the name suggests, it can be obtained by rectifying the tesseract.

As the rectified tesseract, it is the square member of an infinite family of isogonal rectified duoprisms, and could be called the rectified square duoprism. In this representation it is also the convex hull of 2 oppositely oriented semi-uniform square duoprisms where the edges of one square are $\sqrt2 ≈ 1.41421$ times the length of those of the other square.

It is also the convex hull of two perpendicular digonal-square prismantiprismoids (transitional digonal double prismantiprismoid) and is the first member of an infinite family of double prismantiprismoids. It also contains the vertices of two digonal-scalenohedral 8-3 double step prisms.

Gallery

• 

  Wireframe

• 

  Cross-sections

• 

  Net

Vertex coordinates

The vertices of a rectified tesseract of edge length 1 are given by all permutations of:

• $\left(±\frac{\sqrt2}{2},\,±\frac{\sqrt2}{2},\,±\frac{\sqrt2}{2},\,0\right).$

Alternatively, they can be given under D4 symmetry as even sign changes and all permutations of:

• $\left(\frac{3\sqrt2}{4},\,\frac{\sqrt2}{4},\,\frac{\sqrt2}{4},\,\frac{\sqrt2}{4}\right).$

Representations

A rectified tesseract has the following Coxeter diagrams:

• o4x3o3o (full symmetry)
• x3o3x *b3o (D4 symmetry, as small rhombated demitesseract)
• s4o3o3x (as runcic tesseract)
• s4x3o3o (similar to above)
• xxoo3oxxo3ooxx&#xt (A3 axial, tetrahedron-first)
• oqo4xox3ooo&#xt (BC3 axial, cuboctahedron-first)
• qo oq4xo3oo&#zx (BC3×A1 symmetry)
• ox4qo xo4oq&#zx (BC2×BC2 symmetry, rectified square duoprism)
• x(uo)x3o(oo)o3x(uo)x&#xt (A3 axial, cuboctahedron-first)
• oxuxo xoxox4oqoqo&#xt (BC2×A1 axial, square-first)
• oqoqoqo oooxuxo3oxuxooo&#xt (A2×A1 symmetry, vertex-first)

Variations

The rectified tesseract has the following general variations:

• Small rhombated demitesseract - half symmetry, isogonal, 2 types of tetrahedra, cuboctahedra as rhombitetratetrahedra
• Rectified square duoprism - no variations, cuboctahedra have symmetry of recctified square prisms, tetrahedra as tetragonal disphenoids
• Transitional digonal double prismantiprismoid - less symmetric isogonal variant

Related polychora

The rectified tesseract is the colonel of a 5-member regiment. Other members of this regiment include the facetorectified tesseract, hexadecintercepted tesseract, small trisoctachoron, and great trisoctachoron. The first two of these have full B4 symmetry, while the latter two have D4 symmetry only.

When viewed in A3 axial symmetry, the rectified tesseract can be seen as a central truncated tetrahedral cupoliprism with 2 tetrahedron atop truncated tetrahedron segmentochora attached to its bases.

Uniform polychoron compounds composed of rectified tesseracts include:

• Birectified demidistesseract (2)
• Rectified great icositetrachoron (3)
• Rectified great stellated tetracontoctachoron (6)
• Rectified dodecahedronary cubichoron (75)
• Rectified cubichoron (75)

Isogonal derivatives

Substitution by vertices of these following elements will produce these convex isogonal polychora:

• Cuboctahedron (8): Hexadecachoron
• Tetrahedron (16): Tesseract
• Square (24): Icositetrachoron
• Triangle (64): Semi-uniform small disprismatotesseractihexadecachoron
• Edge (96): Semi-uniform small rhombated tesseract

External links

• Bowers, Jonathan. "Category 3: Triangular Rectates" (#42).

• Bowers, Jonathan. "Tessic Isogonals".

• Klitzing, Richard. "rit".

• Quickfur. "The Rectified Tesseract".

• Wikipedia Contributors. "Rectified tesseract".