Regular polychoron
A regular polychoron is a polychoron whose flags are identical under its symmetry group. In 3D Euclidean space, there are 16 finite regular polychora and 1 honeycomb that are not skew, and an unknown number of additional regular polychora that are skew.
Regular convex polychora[edit | edit source]
The regular convex polychora are the 4-dimensional counterparts to the Platonic solids and the regular convex polygons. There are 6 regular convex polychora. Apart from the infinite set of regular convex polygons, there are more regular convex polytopes of rank 4 than of any other rank.
| Solid | Number of facets | Schläfli symbol | Image |
|---|---|---|---|
| 5-cell | 5 | {3,3,3} | 
|
| 8-cell | 8 | {4,3,3} | 
|
| 16-cell | 16 | {3,3,4} | 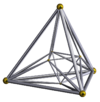
|
| 24-cell | 24 | {3,4,3} | 
|
| 120-cell | 120 | {3,3,5} | 
|
| 600-cell | 600 | {5,3,3} | 
|
Proof of completeness[edit | edit source]
This section needs expansion. You can help by adding to it. |
Recursive geometric proof[edit | edit source]
The following proof shows that the above 6 polychora are the only convex regular polychora, using the completeness of the Platonic solids. For a proof that the Platonic solids are the only regular convex polyhedra, see Regular polyhedron § Geometric proof.
The facet of a regular convex polychoron must be itself a regular convex polyhedron. More subtly, the vertex figure of a regular convex polychoron must also be a regular convex polyhedron. We can see this because the dual of a regular convex polychoron must be itself a regular convex polychoron, and so its vertex figure is dual to the facet of another regular convex polychoron.
Since there are only 5 regular convex polyhedra:
there are only a finite number of ways to combine them with one as the facet and one as the vertex figure. Two polytopes can be combined if the vertex figure of the facet matches the face of the vertex figure. So we can make a polychoron with {5,3} as the facet and {3,4} as the verf because the 3s match, but {3,5} does not match with itself.
There are in total 11 combinations to be checked:
Five of them are not in the above list of 6. And while they are arguably convex they are all apeirochora of differing types and thus not valid regular convex polychora:
- {4,3,4}: Euclidean tessellation
- {3,5,3}: Compact hyperbolic tessellation
- {3,4,5}: Compact hyperbolic tessellation
- {5,3,4}: Compact hyperbolic tessellation
- {5,3,5}: Compact hyperbolic tessellation
Schläfli-Hess polychora[edit | edit source]
There are also 10 finite self-intersecting regular polychora, known as the Schläfli-Hess polychora:
- {3,5,5/2} - Faceted hexacosichoron
- {5,5/2,5} - Great hecatonicosachoron
- {5,3,5/2} - Grand hecatonicosachoron
- {5/2,5,3} - Small stellated hecatonicosachoron
- {5,5/2,3} - Great grand hecatonicosachoron
- {5/2,3,5} - Great stellated hecatonicosachoron
- {5/2,5,5/2} - Grand stellated hecatonicosachoron
- {3,5/2,5} - Great faceted hexacosichoron
- {3,3,5/2} - Grand hexacosichoron
- {5/2,3,3} - Great grand stellated hecatonicosachoron
Proof of completeness[edit | edit source]
Recursive proof[edit | edit source]
This section needs expansion. You can help by adding to it. |
The proof of the completeness of the regular convex polychora can be extended into a wider recursive proof that the 10 Schläfli-Hess polychora above, along with the 6 regular convex polychora, are the only finite planar polychora.
As before the facet and vertex figure of a regular polychoron is a regular polyhedron. The possible components are then:
The valid combinations, excluding those enumerated in the previous proof, are then:
- {3,3,5/2}
- {3,5,5/2}
- {3,5/2,3}
- {3,5/2,5}
- {4,3,5/2}
- {5,3,5/2}
- {5,5/2,3}
- {5,5/2,5}
- {5/2,3,3}
- {5/2,3,4}
- {5/2,3,5}
- {5/2,3,5/2}
- {5/2,5,3}
- {5/2,5,5/2}
Four of these are not among the Schläfli-Hess polychora. We can apply Van Oss's criterion to show that all of these must be infinite dense polychora[1] and are thus discarded:
- {3,5/2,3}
- {4,3,5/2}
- {5/2,3,4}
- {5/2,3,5/2}
Regular compounds[edit | edit source]
This section is empty. You can help by adding to it. |
Regular tesselations[edit | edit source]
Euclidean[edit | edit source]
There is also a single regular honeycomb of 3-dimensional Euclidean space:
- {4,3,4} - Cubic honeycomb
Hyperbolic[edit | edit source]
This section needs expansion. You can help by adding to it. |
There are infinitely many regular honeycombs in 3-dimensional space. These can be classified as compact, paracompact or hypercompact depending on their symmetry group. There are 4 compact and 11 paracompact regular hyperbolic honeycombs, all the remaining honeycombs are hypercompact.
| Image |  |
 |
 |

|
|---|---|---|---|---|
| Schläfli symbol | {5,3,4} | {4,3,5} | {3,5,3} | {5,3,5} |
| Image |  |
 |
 |

|
|---|---|---|---|---|
| Schläfli symbol | {6,3,3} | {4,4,3} | {6,3,4} | {6,3,5} |
| Image |  |
 |
 |

|
| Schläfli symbol | {4,3,6} | {5,3,6} | {3,4,4} | {4,4,4} |
| Image |  |
 |

| |
| Schläfli symbol | {3,3,6} | {3,6,3} | {6,3,6} |
Regular skew polychora[edit | edit source]
Finite regular skew polychora[edit | edit source]
There are 18 finite regular skew polychora. The Petrial tesseract can be obtained as the Petrie dual of the tesseract, and the other 17 regular skew polychora can be obtained by applying κ to the Petrial tesseract or any of the 16 planar polychora above.
- Petrial tesseract <--> Petrial alternative tesseract
- 5-cell <--> Kappa 5-cell
- Tesseract <--> Alternative tesseract
- 16-cell <--> Kappa 16-cell
- 24-cell <--> Kappa 24-cell
- 120-cell <--> Kappa 120-cell
- 600-cell <--> Kappa 600-cell
- Icosahedral 120-cell <--> Kappa icosahedral 120-cell
- Great 120-cell <--> Kappa great 120-cell
- Small stellated 120-cell <--> Kappa small stellated 120-cell
- Great grand 120-cell <--> Kappa great grand 120-cell
- Great stellated 120-cell <--> Kappa great stellated 120-cell
- Grand stellated 120-cell <--> Kappa grand stellated 120-cell
- Great icosahedral 120-cell <--> Kappa great icosahedral 120-cell
- Grand 600-cell <--> Kappa grand 600-cell
- Great grand stellated 120-cell <--> Kappa great grand stellated 120-cell
Regular skew honeycombs[edit | edit source]
This section needs expansion. You can help by adding to it. |

In addition to the single regular planar honeycomb there are 7 regular skew honeycombs in 3-dimensional Euclidean space:
- - Mucubic honeycomb
- - Apeir tetrahedron
- - Petrial apeir tetrahedron
- - Apeir octahedron
- - Petrial apeir octahedron
- - Apeir cube
- - Petrial apeir cube
The mucubic honeycomb is the Petrie dual of the cubic honeycomb.
Skew apeirochora in 4-dimensions[edit | edit source]
The regular polyhedra have several regular apeirohedra spanning 3 dimensions. e.g. the mucube and the blended triangular tiling. One could speculate potentially exists analogous regular apeirochora spanning 4-dimensions, and indeed these do exist.
Blends[edit | edit source]
Regular skew apeirochora in 4 dimensions can be made by blending regular honeycombs with a 2-dimensional polytope. This category gives 16 blends made from the eight regular honeycombs with either the dyad or the apeirogon.
These are analogous to the 12 blended apeirohedra in 3 dimensions.
Pure apeirochora[edit | edit source]
This section is empty. You can help by adding to it. |
External links[edit | edit source]
- Wikipedia contributors. "Regular 4-polytope".
References[edit | edit source]
- ↑ Coxeter (1973:275)
Bibliography[edit | edit source]
- Coxeter, Donald (1973). Regular polytopes (3 ed.). Dover. ISBN 0-486-61480-8. OCLC 798003.
- McMullen, Peter (2004). "Regular Polytopes of Full Rank" (PDF). Discrete Computational Geometry.






