Segmentotope
A segmentotope is an rank-n orbiform (i.e. having a single edge length and a circumscribed hypersphere) prismatoid (i.e. having vertices that are are contained in two parallel (n–1) -dimensional hyperplanes). The convex ones are thereby a subclass of the convex regular-faced polytopes. The term "segmentotope" was first used by R. Klitzing in 2000.[1] Segmentotopes are usually named with the notation "X atop Y" or "X || Y", where X and Y are the two bases. (Note, that for the smaller segmentotopes the choice of the describing axial direction needs not be unique.)
The top and bottom bases of a convex segmentotope are orbiform polytopes. The facets that lace the bases together are segmentotopes of one dimension less. In a non-convex segmentotope, the bases aren't necessarily polytopes; they can be pseudo or even just a non-polytopal collection of elements. The bases are not bount to have rank n-1 , but might have lower dimensionality. In that case they need not be placed concentrically, rather in some cases they could be shifted out as well.
Let be the circumradii of the bases, be the respective shifts, and the height, then the total circumradius can generally be calculated as .
A dyad is the only 1-dimensional segmentotope, because by definition, its vertices are in two different 0-dimensional spaces.
The triangle and square are the only 2-dimensional segmentotopes, since they are the only regular polygons for which two parallel lines (1-dimensional spaces) can be drawn that together intersect all vertices of the polygon.
3 dimensions[edit | edit source]
Convex segmentohedra can be classified as one of the following[citation needed]:
- pyramids (point atop n-gon)
- prisms (n-gon atop n-gon)
- antiprisms (n-gon atop gyro n-gon)
- cupolas (n-gon atop 2n-gon).
Three polyhedra have two different constructions: the tetrahedron (both a 3-gonal pyramid and a 2-gonal antiprism), the triangular prism (both a 3-gonal prism and a 2-gonal cupola), and the square pyramid (both a 4-gonal pyramid and a special construction in none of the above categories, 2-gon atop 3-gon, i.e. as the diminishing of the trigonal antiprism).
| Tetrahedron
(triangular pyramid) |
Pentagrammic prism | Octahedron
(triangular antiprism) |
Square cupola | Blend of 2 triangular prisms | Pentagrammic cuploid |
|---|---|---|---|---|---|
| point atop triangle | pentagram atop pentagram | triangle atop (gyrated) triangle | square atop octagon | compound of 2 digons atop pseudo square | pseudo pentagram atop pentagon |
 |
 |
 |
 |
 |
 |
4 dimensions[edit | edit source]
In a segmentochoron, two polyhedra or lower-dimensional polytopes lie in parallel three-dimensional spaces, and relatively small 3D pyramids, prisms, antiprisms, and/or cupolae connect the two through the 4th dimension.
In the case of the relatively simple octahedron atop cube, six square pyramids are attached to the cube's faces and their apexes connect to the vertices of the octahedron, while eight triangular pyramids (tetrahedra) are attached to the octahedron's faces and connect to the cube's vertices. Twelve digonal antiprisms (further tetrahedra) then fill in the gaps between the triangular faces of the attached pyramids, connecting the corresponding edges of the two base polyhedra.
The prisms with orbiform polyhedron bases are segmentochora. For an orbiform polyhedron with circumradius less than 1, if a pyramid is made from it, the pyramid will be a segmentochoron.
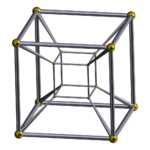
| Tesseract | Octahedral pyramid | Hexagonal antifastegium | Cuboctatruncated cuboctahedral prism | Dodecahedron atop rhombidodecadodecahedron |
|---|---|---|---|---|
| cube atop cube; cubic prism | point atop octahedron | hexagon atop (gyrated) hexagonal prism | cuboctatruncated cuboctahedron atop cuboctatruncated cuboctahedron | |
 |
 |
 |
 |
 |
In general[edit | edit source]
In any dimension , all three of the regular polytopes (the n -simplex, n -hypercube, and n -orthoplex) will be segmentotopes, as point atop n-1 -simplex, n-1 -cube atop n-1 -cube, and n-1 -simplex atop dual n-1 -simplex, respectively.
The prism product of an orbiform polytope and a segmentotope will be another segmentotope. (This includes the simple case of the polytope prism, where the inputted segmentotope is the dyad.)
For an orbiform polytope with circumradius less than 1, if a pyramid is made from it, the pyramid will be a segmentotope.
Alterprisms and antiprisms (if they can be made to have a single edge length) are segmentotopes.
The rectified n -simplex is a segmentotope, as n-1 -simplex atop rectified n-1 -simplex.
Many other segmentotopes can be obtained as slices of uniform polytopes. This is not a complete list of possible ways to obtain segmentotopes.
External links[edit | edit source]
- Klitzing, Richard. "Segmentochora."
References[edit | edit source]
- ↑ Convex Segmentochora, R. Klitzing, Symmetry: Culture and Science Vol. 11, Nos. 1-4, 139-181, 2000





