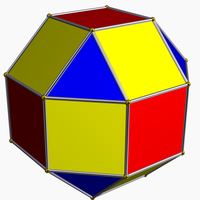
Small rhombicuboctahedron

Small rhombicuboctahedron
(3D model) (OFF file)
Rank	3
Type	Uniform
Notation
Bowers style acronym	Sirco
Coxeter diagram	x4o3x ()
Conway notation	eC
Stewart notation	E4
Elements
Faces	8 triangles 6+12 squares
Edges	24+24
Vertices	24
Vertex figure	Isosceles trapezoid, edge lengths 1, √2, √2, √2
Measures (edge length 1)
Circumradius	${\frac {\sqrt {5+2{\sqrt {2}}}}{2}}\approx 1.39897$
Volume	$2{\frac {6+5{\sqrt {2}}}{3}}\approx 8.71404$
Dihedral angles	4–3: $\arccos \left(-{\frac {\sqrt {6}}{3}}\right)\approx 144.73561^{\circ }$
	4–4: 135°
Central density	1
Number of external pieces	26
Level of complexity	4
Related polytopes
Army	Sirco
Regiment	Sirco
Dual	Deltoidal icositetrahedron
Conjugate	Quasirhombicuboctahedron
Abstract & topological properties
Flag count	192
Euler characteristic	2
Surface	Sphere
Orientable	Yes
Genus	0
Properties
Symmetry	B3, order 48
Flag orbits	4
Convex	Yes
Nature	Tame

The small rhombicuboctahedron, also commonly known as simply the rhombicuboctahedron, or sirco is one of the 13 Archimedean solids. It consists of 8 triangles and 6+12 squares, with one triangle and three squares meeting at each vertex. It also has 6 octagonal pseudofaces. It can be obtained by cantellation of the cube or octahedron, or equivalently by pushing either polyhedron's faces outward and filling the gaps with the corresponding polygons. Rectifying the cuboctahedron gives a semi-uniform variant of the rhombicuboctahedron.

6 of the squares in this figure have full B₂ symmetry, while 12 of them have only K₂ symmetry with respect to the whole polyhedron.

Vertex coordinates

A small rhombicuboctahedron of edge length 1 has vertex coordinates given by all permutations of:

• $\left(\pm {\frac {1+{\sqrt {2}}}{2}},\,\pm {\frac {1}{2}},\,\pm {\frac {1}{2}}\right)$.

Representations

A small rhombicuboctahedron has the following Coxeter diagrams:

• x4o3x () (full symmetry)
• x4s3s () (B₃+ symmetry, is an edge-snub octahedron/edge-alternated great rhombicuboctahedron)
• xxxx4oxxo&#xt (B₂ axial, main square-first)
• xxwoqo3oqowxx&#xt (A₂ axial, triangle-first)
• qo3xx3oq&#zx (A₃ subsymmetry, hull of two opposite truncated tetrahedra)
• wx xx4ox&#zx (B₂×A₁ symmetry)
• wxx xwx xxw&#zx (K₃ symmetry)
• xowqwox xwxwxwx&#xt (K₂ axial)

Semi-uniform variant

The small rhombicuboctahedron has a semi-uniform variant of the form x4o3y that maintains its full symmetry. This variant has 6 squares of side length x, 8 triangles of side length y, and 12 rectangles as faces.

With edges of length a (of squares) and b (of triangles), its circumradius is given by ${\frac {\sqrt {3a^{2}+2b^{2}+2ab{\sqrt {2}}}}{2}}$ and its volume is given by $a^{3}+3ab^{2}+(9a^{2}b+b^{3}){\frac {\sqrt {2}}{3}}$.

It has coordinates given by all permutations of:

• $\left(\pm {\frac {a+b{\sqrt {2}}}{2}},\,\pm {\frac {a}{2}},\,\pm {\frac {a}{2}}\right).$

Variations

Besides the semi-uniform variation, another variation, the pyritosnub cube, can be obtained as an alternated faceting of the great rhombicuboctahedron with pyritohedral symmetry. This faceting has 6 rectangles, 8 triangles, and 12 trapezoids as faces.

Related polyhedra

The small rhombicuboctahedron is the colonel of a three-member regiment that also includes the small cubicuboctahedron and the small rhombihexahedron.

It is possible to diminish the small rhombicuboctahedron by removing square cupolas. In fact, it is the result of attaching two square cupolas to an octagonal prism's bases, and can be called an elongated square orthobicupola. If one is removed the result is the elongated square cupola. If one cupola is rotated by 45º, the result is the elongated square gyrobicupola, or pseudo-rhombicuboctahedron. If the central prism is removed and the two cupolas are connected at their octagonal face, the result is a square orthobicupola.

The rhombisnub rhombicosicosahedron is a uniform polyhedron compound composed of 5 small rhombicuboctahedra.

The überoctoplex is abstractly identical and also isogonal, but is not convex and only has B₃/2 symmetry.

External links

• Bowers, Jonathan. "Polyhedron Category 4: Trapeziverts" (#36).

• Klitzing, Richard. "sirco".
• Quickfur. "The Rhombicuboctahedron".

• Wikipedia contributors. "Rhombicuboctahedron".
• McCooey, David. "Rhombicuboctahedron"

• Hi.gher.Space Wiki Contributors. "Stauroperihedron".