Compound of two great icosahedra

Compound of two great icosahedra
(3D model) (OFF file)
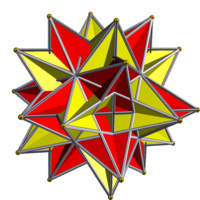Rank	3
Type	Uniform
Notation
Bowers style acronym	Sirsido
Elements
Components	2 great icosahedra
Faces	24 triangles, 16 triangles as 8 hexagrams
Edges	12+48
Vertices	24
Vertex figure	Regular pentagram, edge length 1
Measures (edge length 1)
Circumradius	${\sqrt {\frac {5-{\sqrt {5}}}{8}}}\approx 0.58779$
Inradius	${\frac {3{\sqrt {3}}-{\sqrt {15}}}{12}}\approx 0.11026$
Volume	$5{\frac {3-{\sqrt {5}}}{6}}\approx 0.63661$
Dihedral angle	$\arccos \left({\frac {\sqrt {5}}{3}}\right)\approx 41.81031^{\circ }$
Central density	14
Number of external pieces	264
Level of complexity	36
Related polytopes
Army	Semi-uniform Toe, edge lengths ${\frac {{\sqrt {10}}-{\sqrt {2}}}{4}}$ (squares), ${\frac {3{\sqrt {2}}-{\sqrt {10}}}{4}}$ (between ditrigons)
Regiment	Passipsido
Dual	Compound of two great stellated dodecahedra
Conjugate	Compound of two icosahedra
Convex core	Octatruncated tetrakis hexahedron
Abstract & topological properties
Flag count	240
Orientable	Yes
Properties
Symmetry	B3, order 48
Flag orbits	5
Convex	No
Nature	Tame

The small retrosnub disoctahedron, sirsido, or compound of two great icosahedra is a uniform polyhedron compound. It consists of 40 triangles (8 pairs of which form hexagrams due to following in the same plane), with five faces joining at a vertex.

It can be constructed from the pentagrammatic snub pseudodisoctahedron by replacing each small stellated dodecahedron with the great icosahedron with which it shares its edges.

Gallery

Vertex coordinates

Its vertices are the same as those of its regiment colonel, the pentagrammatic snub pseudodisoctahedron.

External links

• Bowers, Jonathan. "Polyhedron Category C4: Ikers" (#24).

• Klitzing, Richard. "sirsido".
• Wikipedia contributors. "Compound of two great icosahedra".