Small inverted retrosnub icosicosidodecahedron

Small inverted retrosnub icosicosidodecahedron
(3D model) (OFF file)
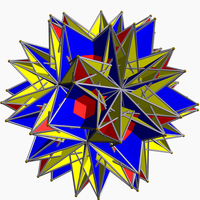Rank	3
Type	Uniform
Space	Spherical
Notation
Bowers style acronym	Sirsid
Coxeter diagram	s5/2s3/2s3/2*a ()
Elements
Faces	60 triangles, 40 triangles as 20 hexagrams, 12 pentagrams
Edges	60+60+60
Vertices	60
Vertex figure	Mirror-symmetric hexagon, edge lengths 1, 1, 1, 1, 1, (√5–1)/2
Measures (edge length 1)
Circumradius	$\frac{\sqrt{13+3\sqrt5-\sqrt{102+46\sqrt5}}}{4} \approx 0.58069$
Volume	$\frac{45+39\sqrt5-5\sqrt{302+150\sqrt5}}{12} \approx 0.49764$
Dihedral angles	5/2–3: $\arccos\left(\sqrt{\frac{15-2\sqrt5-2\sqrt{30\sqrt5-65}}{15}}\right) \approx 44.45753^\circ$
	3–3: $\arccos\left(\frac{\sqrt{3+2\sqrt5}}{3}\right) \approx 24.33196^\circ$
Central density	38
Number of external pieces	3060
Level of complexity	213
Related polytopes
Army	Semi-uniform Tid, edge lengths $\frac{\sqrt{3+2\sqrt5}-\sqrt5}{2}$ (triangles), $\frac{3-\sqrt{3+2\sqrt5}}{2}$ (between dipentagons)
Regiment	Sirsid
Dual	Small hexagrammic hexecontahedron
Conjugate	Small snub icosicosidodecahedron
Convex core	Order-6 truncated pentakis dodecahedron
Abstract & topological properties
Flag count	720
Euler characteristic	–8
Orientable	Yes
Properties
Symmetry	H3, order 120
Convex	No
Nature	Tame

The small inverted retrosnub icosicosidodecahedron, or sirsid, also called the small retrosnub icosicosidodecahedron, is a uniform polyhedron. It consists of 60 snub triangles, 40 more triangles that create 20 hexagrams due to pairs lying in the same plane, and 12 pentagrams. Five triangles and one pentagram meet at each vertex.

In terms of level of complexity, this is the most complex uniform polyhedron.

Vertex coordinates

A small inverted retrosnub icosicosidodecahedron of edge length 1 has vertex coordinates given by all even permutations of:

• $\left(0,\,±\frac{3-\sqrt{3+2\sqrt5}}{4},\,±\frac{\sqrt5-1+\sqrt{6\sqrt5-2}}{8}\right),$
• $\left(±\frac12,\,±\frac{\sqrt{3+2\sqrt5}-\sqrt5}{4},\,±\frac{1-\sqrt5+\sqrt{6\sqrt5-2}}{8}\right),$
• $\left(±\frac{\sqrt5-1}{4},\,±\frac{\sqrt{3+2\sqrt5}-1}{4},\,±\frac{3+\sqrt5-\sqrt{6\sqrt5-2}}{8}\right).$

Representations

A small inverted retrosnub icosicosidodecahedron has the following Coxeter diagrams:

• s3/2s3/2s5/2*a
• o5ß3/2ß (as holosnub)

External links

• Bowers, Jonathan. "Polyhedron Category 6: Snubs" (#74).

• Klitzing, Richard. "sirsid".

• Wikipedia Contributors. "Small retrosnub icosicosidodecahedron".
• McCooey, David. "Small Retrosnub Icosicosidodecahedron"