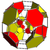
Small disprismatotesseractihexadecachoron

Small disprismatotesseracti-hexadecachoron
(OFF file)
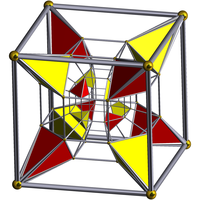Rank	4
Type	Uniform
Space	Spherical
Notation
Bowers style acronym	Sidpith
Coxeter diagram	x4o3o3x ()
Elements
Cells	16 tetrahedra, 32 triangular prisms, 8+24 cubes
Faces	64 triangles, 48+96 squares
Edges	96+96
Vertices	64
Vertex figure	Triangular antipodium, edge lengths 1 (small base), and √2 (large base and sides)
Measures (edge length 1)
Circumradius	$\sqrt{\frac{3+\sqrt2}{2}} ≈ 1.48563$
Hypervolume	$\frac{43+32\sqrt2}{6} ≈ 14.70914$
Dichoral angles	Tet–3–trip: 150°
	Cube–4–trip: $\arccos\left(-\frac{\sqrt6}{3}\right) ≈ 144.73561^\circ$
	Cube–4–cube: 135°
Central density	1
Number of external pieces	80
Level of complexity	8
Related polytopes
Army	Sidpith
Regiment	Sidpith
Dual	Triangular-antitegmatic hexacontatetrachoron
Conjugate	Quasidisprismatotesseracti-hexadecachoron
Abstract & topological properties
Flag count	3072
Euler characteristic	0
Orientable	Yes
Properties
Symmetry	B4, order 384
Convex	Yes
Nature	Tame

The small disprismatotesseractihexadecachoron, square duoexpandoprism, or sidpith, also commonly called the runcinated tesseract, is a convex uniform polychoron that consists of 16 regular tetrahedra, 32 triangular prisms, and 8+24 cubes. 1 tetrahedron, 3 triangular prisms, and 1+3 cubes join at each vertex. It is the result of expanding the cells of either a tesseract or a hexadecachoron outwards, and thus could also be called the runcinated 16-cell.

It is the third in the series of duoexpandoprisms formed as the convex hull of a compound of two perpendicular square-octagonal duoprisms and the only uniform one. Blending it with these duoprisms produces the inverted quasiprismatodishexadecachoron. It additionally contains the vertices and edges of the small rhombicuboctahedral prism.

Gallery

• 

  B4 Coxeter plane projection

• 

  Wireframe

• 

  Net

• 

  Cross-sections

• 

  Cross-section animation

Vertex coordinates

Coordinates for the vertices of a small disprismatotesseractihexadecachoron with edge length 1 are given by all permutations of:

• $\left(±\frac{1+\sqrt2}{2},\,±\frac12,\,±\frac12,\,±\frac12\right).$

Representations

A small disprismatotesseractihexadecachoron has the following Coxeter diagrams:

• x4o3o3x (full symmetry)
• xxxx4oooo3oxxo&#xt (BC3 axial, cube-first)
• xxxowoqo3ooqooqoo3oqowoxxx&#xt (A3 axial, tetrahedron-first)
• xowqwox xxxxxxx4oxoxoxo&#xt (BC2×A1 symmetry, cube-first)
• qo3oo3oq *b3xx&#zx (D4 symmetry)
• wx xx4oo3ox&#zx (BC3×A1 symmetry)
• xo4xx ox4xx&#zx (BC3×BC2 symmetry, square duoexpandoprism)
• wxxx xwxx xxwx xxxw&#zx (A1×A1×A1×A1 symmetry)

Semi-uniform variant

The small disprismatotesseractihexadecachoron has a semi-uniform variant of the form x4o3o3y that maintains its full symmetry. This variant uses 8 cubes of size x, 16 tetrahedra of size y, 32 semi-uniform triangular prisms of form x y3o, and 24 semi-uniform square prisms of form y x4o as cells, with 2 edge lengths.

With edges of length a (of cubes) and b (of tetrahedra), its circumradius is given by $\sqrt{\frac{2a^2+b^2+ab\sqrt2}{2}}$ and its hypervolume is given by $\frac{6a^4+36a^2b^2+b^4+(24a^3b+8ab^3)\sqrt2}{6}$.

It has coordinates given by all permutations of:

• $\left(±\frac{a+b\sqrt2}{2},\,±\frac{a}{2},\,±\frac{a}{2},\,±\frac{a}{2}\right).$

Variations

The uniform small disprismatotesseractihexadecachoron, and indeed the semi-uniform variants, are a special class of the general isogonal square duoexpandoprism. This general variant has as cells 2 sets of 8 square prisms, 16 rectangular trapezoprisms, 32 wedges, and 16 tetragonal disphenoids as cells. They can generally be obtained as the convex hull of 2 orthogonal square-ditetragonal duoprisms.

This is one of a total of five polychora that can be obtained as the convex hull of two orthogonal square-ditetragonal duoprisms. To produce variants of this polychoron, if the polychoron is written as ao4bc oa4cb&#zy, c must be in the range $c < b+\frac{a}{\sqrt2}$. It generally has circumradius $\sqrt{\frac{2a^2+2b^2+2ab\sqrt2+c^2}{2}}$.

Related polychora

The small disprismatotesseractihexadecachoron is the colonel of a regiment with a total of 8 uniform and 6 scaliform members. Of these members, 7 have full tesseractic symmetry, namely sidpith, stefacoth, shafipto, steth, dippit, snappoth, and snipto. The eighth uniform member iquipadah and the 6 scaliform members have square duoprism symmetry. The compound octagonal diorthoprism can be edge-inscribed in this polychoron.

A small disprismatotesseractihexadecachoron can be constructed from a small rhombicuboctahedral prism by attaching cube atop small rhombicuboctahedron segmentochora to its bases. The cap from the set of 24 cubes is the square cupofastegium.

Uniform polychoron compounds composed of small disprismatotesseractihexadecachora include:

• Small prismated great icositetrachoron (3)
• Small prismated great stellated tetracontoctachoron (6)
• Small prismated dodecahedronary cubichoron (75)

{{o4o3o3o truncations}

External links

• Bowers, Jonathan. "Category 11: Antipodiumverts" (#447).

• Bowers, Jonathan. "Tessic Isogonals".

• Klitzing, Richard. "sidpith".

• Quickfur. "The Runcinated Tesseract".

• Wikipedia Contributors. "Runcinated tesseract".