Square tiling prism

Square tiling prism
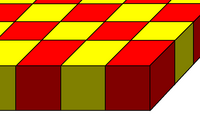Rank	4
Type	Uniform
Space	Euclidean
Notation
Coxeter diagram
Elements
Cells	MN cubes, 2 square tilings
Faces	2MN+2MN squares
Edges	MN+4MN
Vertices	2MN
Vertex figure	Square pyramid
Related polytopes
Army	*
Regiment	*
Dual	Square tiling tegum
Abstract & topological properties
Orientable	Yes
Properties
Symmetry	R3×A1
Convex	Yes
Nature	Tame

The square tiling prism or cubic slab honeycomb is a prismatic uniform honeycomb of the Euclidean plane. It consists of 2 square tilings and ∞ cubes. Each vertex joins 1 square tiling and 4 cubes. It is a prism based on the square tiling.

It appears as a segment of the cubic honeycomb.

Vertex coordinates

A square tiling prism of edge length 1 has vertex coordinates given by, where $i,\,j$ range over the integers:

• $\left(\pm {\tfrac {1}{2}},\,i,\,j,\,0\right)$

Semi-uniform variant

The apeirogonal prism has a semi-uniform variant of the form x y4o4o that maintains its full symmetry. This variant uses square prisms as its sides.

External links

• Wikipedia contributors. "Convex uniform honeycomb#Frieze forms".