Stella octangula

Stella octangula
(3D model) (OFF file)
Rank	3
Type	Regular
Space	Spherical
Notation
Bowers style acronym	So
Coxeter diagram	β4o3o ()
Elements
Components	2 tetrahedra
Faces	8 triangles
Edges	12
Vertices	8
Vertex figure	Equilateral triangle, edge length 1
Measures (edge length 1)
Circumradius	$\frac{\sqrt6}{4} \approx 0.61237$
Inradius	$\frac{\sqrt6}{12} \approx 0.20412$
Volume	$\frac{\sqrt2}{6} \approx 0.23570$
Dihedral angle	$\arccos\left(\frac13\right) \approx 70.52877^\circ$
Central density	2
Number of external pieces	24
Level of complexity	3
Related polytopes
Army	Cube, edge length $\frac{\sqrt2}{2}$
Regiment	So
Dual	Stella octangula
Conjugate	None
Convex core	Octahedron
Abstract & topological properties
Flag count	48
Schläfli type	{3,3}
Orientable	Yes
Properties
Symmetry	B3, order 48
Convex	No
Nature	Tame

The stella octangula, stellated octahedron, so, or compound of two tetrahedra is a regular polyhedron compound. It's made out of 8 triangles, 3 joining at each vertex. It can be constructed by taking a tetrahedron and overlaying it with its central inversion. Alternatively, it can be created by stellating the octahedron.

It can also be considered an antiprism based on the compound of two digons {4/2}.

Its quotient prismatic equivalent is the hexadecachoron, which is four-dimensional.

Gallery

Representations

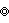
• (full symmetry)
• (β2β4o)
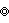
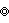
• (β2β2β)
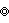
• xo3oo3ox

Vertex coordinates

The vertices of a stella octangula of edge length 1 can be given by:

• $\left(\pm\frac{\sqrt2}{4},\,\pm\frac{\sqrt2}{4},\,\pm\frac{\sqrt2}{4}\right).$

These arise from the fact that a tetrahedron can be constructed as the alternation of the cube. Taking even changes of sign and odd changes of sign reconstructs the two component tetrahedra.

Alternate coordinates can be derived from those of the triangle, by considering the tetrahedron as a triangular pyramid:

• $\pm\left(\pm\frac12,\,-\frac{\sqrt3}{6},\,-\frac{\sqrt6}{12}\right)$,
• $\pm\left(0,\,\frac{\sqrt3}{3},\,-\frac{\sqrt6}{12}\right)$,
• $\left(0,\,0,\,\pm\frac{\sqrt6}{4}\right)$.

These are more complicated, but generalize to two-simplex compounds of any dimension.

External links

• Bowers, Jonathan. "Polyhedron Category C1: Compound Regulars" (#1).

• Klitzing, Richard. "so".

• Wikipedia Contributors. "Stellated octahedron".