Zonotope

An example of the Minkowski sum in 2D. The four line segments (left) that generate the octagon (right) are visible as the octagon's edges.

A zonotope is a polytope that is the Minkowski sum of a set of vectors. These vectors are called its generators.

A zonotope can also be defined as a convex polytope whose facets are all zonotopes and which has central inversion symmetry.

Properties

The faces of a zonotope always have an even number of edges, and the facets of a zonotope are themselves zonotopes.

An n-dimensional zonotope can always be dissected into "primitive" zonotopes (which are n-parallelotopes, or the generalization of parallelepipeds to n dimensions).

Examples

The lowest possible symmetry of a 2D zonotope or higher-dimensional zonotope's face.

2D (zonogons)

All polygons with point symmetry (that is, they have a symmetry that rotates them 180° about the center) are zonotopes, and all convex regular 2n-gons are zonotopes. These are usually found as the faces of higher-dimensional zonotopes.

3D (zonohedra)

Of the uniform polyhedra, the cube and the three omnitruncates (the truncated octahedron, truncated cuboctahedron, and truncated icosidodecahedron) are zonotopes.

Two of the uniform dual polyhedra - the rhombic dodecahedron and rhombic triacontahedron - are also zonotopes.

Removing one or two generators from the rhombic triacontahedron results in the rhombic icosahedron and Bilinski dodecahedron, respectively. Both are also zonotopes.

The prisms of 2D zonotopes are zonotopes as well.

4D (zonochora)

Of the uniform polychora, the tesseract, great prismatodecachoron, great disprismatotesseractihexadecachoron, truncated icositetrachoron, great prismatotetracontoctachoron, and great disprismatohexacosihecatonicosachoron are zonotopes.

Duoprisms of two 2n-gons are also zonotopes, as are the prisms of 3D zonotopes.

Zonohedrification

A 3-dimensional zonotope composed of 132 rhombi. It is the zonohedrification of the rhombicuboctahedron.

Zonohedrification is an operation upon a polytope (like truncation, the dual, or many others) that regards the vertices of the starting polytope as vectors (originating from the polytope's center), then uses those vectors to generate a zonotope. Parallel vectors are ignored, leaving only one in each direction.

Note that a polytope does not have to be a zonotope to be zonohedrified.

Zonohedrifications in 3D

Input polyhedron		Generators made	Output polyhedron
	tetrahedron	4		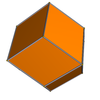rhombic dodecahedron
	cube	4		rhombic dodecahedron
	octahedron	3		cube
	dodecahedron	10		rhombic enneacontahedron
	icosahedron	6		rhombic triacontahedron
	cuboctahedron	6		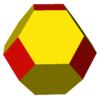truncated octahedron
	icosidodecahedron	15		truncated icosidodecahedron

External links

• Hi.gher.Space Wiki Contributors. "Zonotope".
• Wikipedia Contributors. "Zonohedron".