Zonotope

An example of the Minkowski sum in 2D. The four line segments (left) that generate the octagon (right) are visible as the octagon's edges.

A zonotope is a convex polytope that is the Minkowski sum of a set of closed line segments, called its generators.

A zonotope can also be defined as a convex polytope whose facets are all zonotopes and which has central inversion symmetry.

Properties

The faces of a zonotope always have an even number of edges, and the facets of a zonotope are themselves zonotopes.

An n-dimensional zonotope can always be dissected into "primitive" zonotopes (which are n-parallelotopes, or the generalization of parallelograms and parallelepipeds to n dimensions).

Examples

The lowest possible symmetry of a 2D zonotope or higher-dimensional zonotope's face.

2D (zonogons)

All polygons with point symmetry (that is, they have a symmetry that rotates them 180° about the center) are zonotopes, and all convex regular 2n-gons are zonotopes. These are usually found as the faces of higher-dimensional zonotopes.

3D (zonohedra)

Of the convex uniform polyhedra, the omnitruncates (the truncated octahedron, truncated cuboctahedron, truncated icosidodecahedron and the even-gonal prisms, esp. the cube) are zonotopes.

Two of the uniform dual polyhedra - the rhombic dodecahedron and rhombic triacontahedron - are also zonotopes.

Removing one or two generators from the rhombic triacontahedron results in the rhombic icosahedron and Bilinski dodecahedron, respectively. Both are also zonotopes.

The prism of any 2D zonotope is a 3D zonotope as well.

4D (zonochora)

Of the uniform polychora, the tesseract, great prismatodecachoron, great disprismatotesseractihexadecachoron, truncated icositetrachoron, great prismatotetracontoctachoron, and great disprismatohexacosihecatonicosachoron are zonotopes.

Duoprisms of two 2n-gons are also zonotopes, as are the prisms of 3D zonotopes.

Zonohedrification

A 3-dimensional zonotope composed of 132 rhombi. It is the zonohedrification of the rhombicuboctahedron.

Take any convex polytope P with a well-defined center, and connect every vertex to the center using line segments. The Minkowski sum of these line segments is the zonohedrification of P, a term coined by George Hart. Several zonohedrifications are pictured below.

Zonohedrifications in 3D

Input polyhedron		Generators made	Output polyhedron
	tetrahedron	4		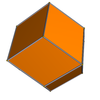rhombic dodecahedron
	cube	4		rhombic dodecahedron
	octahedron	3		cube
	dodecahedron	10		rhombic enneacontahedron
	icosahedron	6		rhombic triacontahedron
	cuboctahedron	6		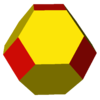truncated octahedron
	icosidodecahedron	15		truncated icosidodecahedron

External links

• Hi.gher.Space Wiki Contributors. "Zonotope".
• Wikipedia Contributors. "Zonohedron".